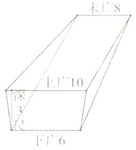
《九章算术》是东方数学思想之源，在卷五《商功》中有以下问题：今有羡除，下广六尺，上广一丈，深三尺，末广八尺，无深，袤七尺，问积几何？译文：如图所示的几何体是三个侧面皆为等腰梯形，其他两面为直角三角形的五面体，（前端）下宽6尺，上宽一丈，深3尺，末端宽8尺，无深，长7尺，则它的体积是立方尺．

2019-05-05

下载本文

《九章算术》是东方数学思想之源，在卷五《商功》中有以下问题：今有羡除，下广六尺，上广一丈，深三尺，末广八尺，无深，袤七尺，问积几何？译文：如图所示的几何体是三个侧面皆为等腰梯形，其他两面为直角三角形的五面体，（前端）下宽6尺，上宽一丈，深3尺，末端宽8尺，无深，长7尺，则它的体积是___立方尺．
作业帮

优质解答

如图，五面体EF-ABCD中，四边形ADEF，ABCD，EFBC均为等腰梯形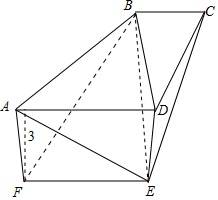，作业帮

EF∥AD∥BC，△ABF，△CDE均为直角三角形，
EF=6，AD=10，BC=8，
EF到平面ABCD的距离为3，AD与BC的距离为7，
连接BE，BD，AE，
得到三个三棱锥，设三棱锥BAEF的体积为V₁，三棱锥BAED的体积为V₂，三棱锥BDEC的体积为V₃，
则V3=

1

3

×

1

2

×8×7×3=28，V2=

1

3

×

1

2

×10×7×3=35，
V1=

1

3

×

1

2

×6×3×7=21．
∴五面体的体积：V=V₁+V₂+V₃=28+35+21=84（立方尺）．
故答案为：84．如图，五面体EF-ABCD中，四边形ADEF，ABCD，EFBC均为等腰梯形，作业帮

EF∥AD∥BC，△ABF，△CDE均为直角三角形，
EF=6，AD=10，BC=8，
EF到平面ABCD的距离为3，AD与BC的距离为7，
连接BE，BD，AE，
得到三个三棱锥，设三棱锥BAEF的体积为V₁，三棱锥BAED的体积为V₂，三棱锥BDEC的体积为V₃，
则V3=

1

3

×

1

2

×8×7×3=28，V2=

1

3

×

1

2

×10×7×3=35，
V1=

1

3

×

1

2

×6×3×7=21．
∴五面体的体积：V=V₁+V₂+V₃=28+35+21=84（立方尺）．
故答案为：84．