优质解答
电场强度和电势都是描述电场性质的物理量,它们二者均与检验电荷无关,那我们就以正电荷为例进行讨论.
场强不必多说.电势:描述电场中(电场赋予电荷的)电势能的物理量,同时也是描述电场(对电荷的)做功能力的物理量.电场中某点的电势,大小上等于电势能与电荷量的比值;也等于电荷从此点移动到零势能点的过程中,电场力做的功与电荷量的比值.由此我们可以分析出,某点电势既与该点场强有关,也与零势能点的选取有关.
零势能点的选取是任意的.但我们通常选用“无穷远处”.所谓“正电荷周围电势为正”、“负电荷周围电势为负”也是基于此假设.根据你的问题描述,第一题显然是选择“无穷远处”为零势能点.
那么在选定了零势能点后,某点的电势似乎就只与该点的场强有关了.在匀强电场中确实如此,利用公式做简单推导即可得知,即:
φ= ES (φ:电势;E:场强;S:“测试点”到“零势能点”的“有效位移”).
但是,对于其他情况,却没这么简单.确实,在选定了零势能点之后,电场中各个点的电势就是一个固定值了.某点的电势确实只与该点的“位置”有关,但它却绝不是只与该点的“场强”有关,它还与“从此点到零势能点之间各点”的“场强”有关.
我们知道,功(包括电场力做的功)是“力”在“空间”上的积累效应,力在某一过程中所做的功,与该过程中每一点处力的大小和方向都有关.对与匀强电场,其实是恒力在做功,所以,电场力做功只有位移有关.但对于非匀强电场,某点场强为零,并不代表电荷从该点移动到零势能点的过程电场力做的“总功”为零,因为,做功“途中”各点的场强未必为零.
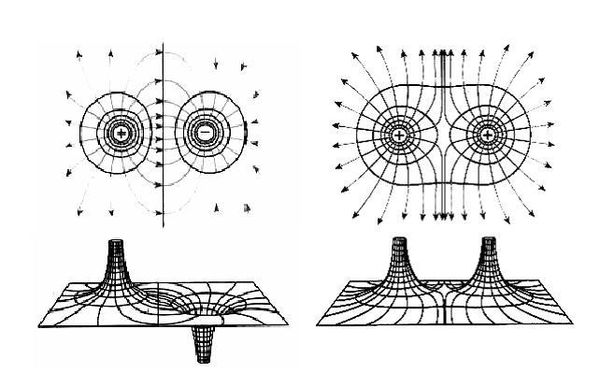
你的第一个问题中,两个等量同种电荷连线的中点就是这样的点.该点场强为零,可是,当一个正电荷从此点移动到零势能点(无穷远处)时,比如,沿着两电荷连线的垂直平分线,向上或向下运动,该过程中电场是要做正功的,电势能是要减少的,因此电势也会减少,这就说明该点的电势为正.从这个电场的等势面图中即可看出,电场的零势能点在无穷远处,而这个点的位置是高于垂直平分线上其他点的,自然高于无穷远处的零势能点.
从上面可以看出:“场强为零的点,电势未必为零”,那么“电势为零的点,场强是否为零”呢?答案也是否定的,例子就是你的第二个问题.两个等量异种电荷,它们连线的垂直平分线上的各点,场强不为零,但各点的电势均为零.当然,前提也是以“无穷远处”为零势能点.我们可以画出这个电场的电场线和等势面.很明显,这条垂直平分线就是一个等势面,电荷在同一等势面上运动,电场是不做功的(因为“力”与“位移”始终是垂直的),所以,电荷沿着这条线移动到无穷远处,电势能不变,即电势不变,恒为零.
可是,很明显,这条垂直平分线上的各点的场强不为零,其大小随着离两电荷中心线的距离的增大而减小,其方向垂直于该垂直平分线,指向负电荷一方.所以,这上面的正电荷向负电荷一方移动时,电场力必然做正功,电势能必然减少,因此负电荷一方的电势是比零电势更小的负电势.所以,“电势为零的点,场强未必为零”.当然,这和零势能点的选取有关.
对于你所问的“两点电势如何比较”,你可以这样做:将一正电荷从 A 点移动到 B 点,看电场力做的总功.若总功为正,说明电势能减少了,因此电势减少
了,即 A 点电势高于 B 点;反之,A 点电势低于 B 点.此法适用于各类电场.从电场的等势面图中也可看出各点电势情况:等势面上的各点,电势相等;沿电场线方向,电势始终减小.
 电场强度和电势都是描述电场性质的物理量,它们二者均与检验电荷无关,那我们就以正电荷为例进行讨论.
电场强度和电势都是描述电场性质的物理量,它们二者均与检验电荷无关,那我们就以正电荷为例进行讨论.
场强不必多说.电势:描述电场中(电场赋予电荷的)电势能的物理量,同时也是描述电场(对电荷的)做功能力的物理量.电场中某点的电势,大小上等于电势能与电荷量的比值;也等于电荷从此点移动到零势能点的过程中,电场力做的功与电荷量的比值.由此我们可以分析出,某点电势既与该点场强有关,也与零势能点的选取有关.
零势能点的选取是任意的.但我们通常选用“无穷远处”.所谓“正电荷周围电势为正”、“负电荷周围电势为负”也是基于此假设.根据你的问题描述,第一题显然是选择“无穷远处”为零势能点.
那么在选定了零势能点后,某点的电势似乎就只与该点的场强有关了.在匀强电场中确实如此,利用公式做简单推导即可得知,即:
φ= ES (φ:电势;E:场强;S:“测试点”到“零势能点”的“有效位移”).
但是,对于其他情况,却没这么简单.确实,在选定了零势能点之后,电场中各个点的电势就是一个固定值了.某点的电势确实只与该点的“位置”有关,但它却绝不是只与该点的“场强”有关,它还与“从此点到零势能点之间各点”的“场强”有关.
我们知道,功(包括电场力做的功)是“力”在“空间”上的积累效应,力在某一过程中所做的功,与该过程中每一点处力的大小和方向都有关.对与匀强电场,其实是恒力在做功,所以,电场力做功只有位移有关.但对于非匀强电场,某点场强为零,并不代表电荷从该点移动到零势能点的过程电场力做的“总功”为零,因为,做功“途中”各点的场强未必为零.
你的第一个问题中,两个等量同种电荷连线的中点就是这样的点.该点场强为零,可是,当一个正电荷从此点移动到零势能点(无穷远处)时,比如,沿着两电荷连线的垂直平分线,向上或向下运动,该过程中电场是要做正功的,电势能是要减少的,因此电势也会减少,这就说明该点的电势为正.从这个电场的等势面图中即可看出,电场的零势能点在无穷远处,而这个点的位置是高于垂直平分线上其他点的,自然高于无穷远处的零势能点.
从上面可以看出:“场强为零的点,电势未必为零”,那么“电势为零的点,场强是否为零”呢?答案也是否定的,例子就是你的第二个问题.两个等量异种电荷,它们连线的垂直平分线上的各点,场强不为零,但各点的电势均为零.当然,前提也是以“无穷远处”为零势能点.我们可以画出这个电场的电场线和等势面.很明显,这条垂直平分线就是一个等势面,电荷在同一等势面上运动,电场是不做功的(因为“力”与“位移”始终是垂直的),所以,电荷沿着这条线移动到无穷远处,电势能不变,即电势不变,恒为零.
可是,很明显,这条垂直平分线上的各点的场强不为零,其大小随着离两电荷中心线的距离的增大而减小,其方向垂直于该垂直平分线,指向负电荷一方.所以,这上面的正电荷向负电荷一方移动时,电场力必然做正功,电势能必然减少,因此负电荷一方的电势是比零电势更小的负电势.所以,“电势为零的点,场强未必为零”.当然,这和零势能点的选取有关.
对于你所问的“两点电势如何比较”,你可以这样做:将一正电荷从 A 点移动到 B 点,看电场力做的总功.若总功为正,说明电势能减少了,因此电势减少
了,即 A 点电势高于 B 点;反之,A 点电势低于 B 点.此法适用于各类电场.从电场的等势面图中也可看出各点电势情况:等势面上的各点,电势相等;沿电场线方向,电势始终减小.

场强不必多说.电势:描述电场中(电场赋予电荷的)电势能的物理量,同时也是描述电场(对电荷的)做功能力的物理量.电场中某点的电势,大小上等于电势能与电荷量的比值;也等于电荷从此点移动到零势能点的过程中,电场力做的功与电荷量的比值.由此我们可以分析出,某点电势既与该点场强有关,也与零势能点的选取有关.
零势能点的选取是任意的.但我们通常选用“无穷远处”.所谓“正电荷周围电势为正”、“负电荷周围电势为负”也是基于此假设.根据你的问题描述,第一题显然是选择“无穷远处”为零势能点.
那么在选定了零势能点后,某点的电势似乎就只与该点的场强有关了.在匀强电场中确实如此,利用公式做简单推导即可得知,即:
φ= ES (φ:电势;E:场强;S:“测试点”到“零势能点”的“有效位移”).
但是,对于其他情况,却没这么简单.确实,在选定了零势能点之后,电场中各个点的电势就是一个固定值了.某点的电势确实只与该点的“位置”有关,但它却绝不是只与该点的“场强”有关,它还与“从此点到零势能点之间各点”的“场强”有关.
我们知道,功(包括电场力做的功)是“力”在“空间”上的积累效应,力在某一过程中所做的功,与该过程中每一点处力的大小和方向都有关.对与匀强电场,其实是恒力在做功,所以,电场力做功只有位移有关.但对于非匀强电场,某点场强为零,并不代表电荷从该点移动到零势能点的过程电场力做的“总功”为零,因为,做功“途中”各点的场强未必为零.
你的第一个问题中,两个等量同种电荷连线的中点就是这样的点.该点场强为零,可是,当一个正电荷从此点移动到零势能点(无穷远处)时,比如,沿着两电荷连线的垂直平分线,向上或向下运动,该过程中电场是要做正功的,电势能是要减少的,因此电势也会减少,这就说明该点的电势为正.从这个电场的等势面图中即可看出,电场的零势能点在无穷远处,而这个点的位置是高于垂直平分线上其他点的,自然高于无穷远处的零势能点.
从上面可以看出:“场强为零的点,电势未必为零”,那么“电势为零的点,场强是否为零”呢?答案也是否定的,例子就是你的第二个问题.两个等量异种电荷,它们连线的垂直平分线上的各点,场强不为零,但各点的电势均为零.当然,前提也是以“无穷远处”为零势能点.我们可以画出这个电场的电场线和等势面.很明显,这条垂直平分线就是一个等势面,电荷在同一等势面上运动,电场是不做功的(因为“力”与“位移”始终是垂直的),所以,电荷沿着这条线移动到无穷远处,电势能不变,即电势不变,恒为零.
可是,很明显,这条垂直平分线上的各点的场强不为零,其大小随着离两电荷中心线的距离的增大而减小,其方向垂直于该垂直平分线,指向负电荷一方.所以,这上面的正电荷向负电荷一方移动时,电场力必然做正功,电势能必然减少,因此负电荷一方的电势是比零电势更小的负电势.所以,“电势为零的点,场强未必为零”.当然,这和零势能点的选取有关.
对于你所问的“两点电势如何比较”,你可以这样做:将一正电荷从 A 点移动到 B 点,看电场力做的总功.若总功为正,说明电势能减少了,因此电势减少
了,即 A 点电势高于 B 点;反之,A 点电势低于 B 点.此法适用于各类电场.从电场的等势面图中也可看出各点电势情况:等势面上的各点,电势相等;沿电场线方向,电势始终减小.
 电场强度和电势都是描述电场性质的物理量,它们二者均与检验电荷无关,那我们就以正电荷为例进行讨论.
电场强度和电势都是描述电场性质的物理量,它们二者均与检验电荷无关,那我们就以正电荷为例进行讨论.场强不必多说.电势:描述电场中(电场赋予电荷的)电势能的物理量,同时也是描述电场(对电荷的)做功能力的物理量.电场中某点的电势,大小上等于电势能与电荷量的比值;也等于电荷从此点移动到零势能点的过程中,电场力做的功与电荷量的比值.由此我们可以分析出,某点电势既与该点场强有关,也与零势能点的选取有关.
零势能点的选取是任意的.但我们通常选用“无穷远处”.所谓“正电荷周围电势为正”、“负电荷周围电势为负”也是基于此假设.根据你的问题描述,第一题显然是选择“无穷远处”为零势能点.
那么在选定了零势能点后,某点的电势似乎就只与该点的场强有关了.在匀强电场中确实如此,利用公式做简单推导即可得知,即:
φ= ES (φ:电势;E:场强;S:“测试点”到“零势能点”的“有效位移”).
但是,对于其他情况,却没这么简单.确实,在选定了零势能点之后,电场中各个点的电势就是一个固定值了.某点的电势确实只与该点的“位置”有关,但它却绝不是只与该点的“场强”有关,它还与“从此点到零势能点之间各点”的“场强”有关.
我们知道,功(包括电场力做的功)是“力”在“空间”上的积累效应,力在某一过程中所做的功,与该过程中每一点处力的大小和方向都有关.对与匀强电场,其实是恒力在做功,所以,电场力做功只有位移有关.但对于非匀强电场,某点场强为零,并不代表电荷从该点移动到零势能点的过程电场力做的“总功”为零,因为,做功“途中”各点的场强未必为零.
你的第一个问题中,两个等量同种电荷连线的中点就是这样的点.该点场强为零,可是,当一个正电荷从此点移动到零势能点(无穷远处)时,比如,沿着两电荷连线的垂直平分线,向上或向下运动,该过程中电场是要做正功的,电势能是要减少的,因此电势也会减少,这就说明该点的电势为正.从这个电场的等势面图中即可看出,电场的零势能点在无穷远处,而这个点的位置是高于垂直平分线上其他点的,自然高于无穷远处的零势能点.
从上面可以看出:“场强为零的点,电势未必为零”,那么“电势为零的点,场强是否为零”呢?答案也是否定的,例子就是你的第二个问题.两个等量异种电荷,它们连线的垂直平分线上的各点,场强不为零,但各点的电势均为零.当然,前提也是以“无穷远处”为零势能点.我们可以画出这个电场的电场线和等势面.很明显,这条垂直平分线就是一个等势面,电荷在同一等势面上运动,电场是不做功的(因为“力”与“位移”始终是垂直的),所以,电荷沿着这条线移动到无穷远处,电势能不变,即电势不变,恒为零.
可是,很明显,这条垂直平分线上的各点的场强不为零,其大小随着离两电荷中心线的距离的增大而减小,其方向垂直于该垂直平分线,指向负电荷一方.所以,这上面的正电荷向负电荷一方移动时,电场力必然做正功,电势能必然减少,因此负电荷一方的电势是比零电势更小的负电势.所以,“电势为零的点,场强未必为零”.当然,这和零势能点的选取有关.
对于你所问的“两点电势如何比较”,你可以这样做:将一正电荷从 A 点移动到 B 点,看电场力做的总功.若总功为正,说明电势能减少了,因此电势减少
了,即 A 点电势高于 B 点;反之,A 点电势低于 B 点.此法适用于各类电场.从电场的等势面图中也可看出各点电势情况:等势面上的各点,电势相等;沿电场线方向,电势始终减小.
