物理
如图所示，CD左侧存在场强大小为E=mgq，方向水平向左的匀强电场，一个质量为m、电荷量为q的光滑绝缘小球，从底边BC长L，倾角α=53°的直角三角形斜面顶端A点由静止开始下滑，运动到斜面底端C点后进入一细管内（C处为一小段长度可忽略的圆弧，圆管内径略大于小球直径），恰能到达D点，随后从D离开后落回到斜面P点，重力加速度为g（sin53°=0.8，cos53°=0.6）．（1）求DA两点间的电势UDA；（2）求圆管半径r；（3）求小球从D点运动到P点的时间t．

2019-06-26

如图所示，CD左侧存在场强大小为E=
mg
q
，方向水平向左的匀强电场，一个质量为m、电荷量为q的光滑绝缘小球，从底边BC长L，倾角α=53°的直角三角形斜面顶端A点由静止开始下滑，运动到斜面底端C点后进入一细管内（C处为一小段长度可忽略的圆弧，圆管内径略大于小球直径），恰能到达D点，随后从D离开后落回到斜面P点，重力加速度为g（sin53°=0.8，cos53°=0.6）．

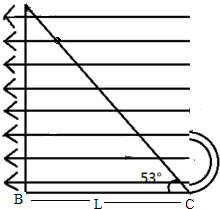
（1）求DA两点间的电势UDA；
（2）求圆管半径r；
（3）求小球从D点运动到P点的时间t．
优质解答
（1）有电势差和场强的关系：u=Ed可知：UDA=Ed=
mg
q
L，
（2）小球恰好经过D点，则小球在D点的速度为0，有动能定理可知：mgLtan53°-EqL-mg2r=0-0，解得：r=
1
6
L，
（3）小球离开D点后，水平方向和竖直方向上受力大小相等，大小均为mg，故水平位移为x=
1
2
at2=
1
2
gt2，竖直位移也为x，轨迹与竖直方向夹角为45°，故根据几何关系可得：x=
L
3
-xtan53°，带入数据得：
1
2
gt2=
L
3
-
1
2
gt2tan53°，解得：t=
2L
7g

答：（1）求DA两点间的电势UDA为
mgL
q
；
（2）求圆管半径r为
L
3
；
（3）求小球从D点运动到P点的时间t为
2L
7g
． （1）有电势差和场强的关系：u=Ed可知：UDA=Ed=
mg
q
L，
（2）小球恰好经过D点，则小球在D点的速度为0，有动能定理可知：mgLtan53°-EqL-mg2r=0-0，解得：r=
1
6
L，
（3）小球离开D点后，水平方向和竖直方向上受力大小相等，大小均为mg，故水平位移为x=
1
2
at2=
1
2
gt2，竖直位移也为x，轨迹与竖直方向夹角为45°，故根据几何关系可得：x=
L
3
-xtan53°，带入数据得：
1
2
gt2=
L
3
-
1
2
gt2tan53°，解得：t=
2L
7g

答：（1）求DA两点间的电势UDA为
mgL
q
；
（2）求圆管半径r为
L
3
；
（3）求小球从D点运动到P点的时间t为
2L
7g
．
相关问答