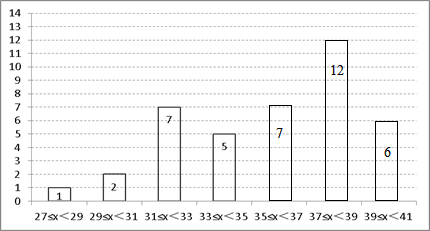
（2014•武汉四月调考）菲尔兹奖（Fields Medal）是享有崇高声誉的数学大奖，每四年颁奖一次，颁给二至四名成就显著的年轻数学家．获奖者当年不能超过四十岁．对获奖者获奖时的年龄进行统计，整理成下面的表格和统计图．年龄段（岁） 27≤x＜29 29≤x＜31 31≤x＜33 33≤x＜35 35≤x＜37 37≤x＜39 39≤x＜41 频数（人） 1 2 7 5 a b c 频率 0.025 0.175 0.1

2019-04-13

下载本文

（2014•武汉四月调考）菲尔兹奖（Fields Medal）是享有崇高声誉的数学大奖，每四年颁奖一次，颁给二至四名成就显著的年轻数学家．获奖者当年不能超过四十岁．对获奖者获奖时的年龄进行统计，整理成下面的表格和统计图．

年龄段（岁）	27≤x＜29	29≤x＜31	31≤x＜33	33≤x＜35	35≤x＜37	37≤x＜39	39≤x＜41
频数（人）	1	2	7	5	a	b	c
频率	0.025				0.175		0.15

（1）直接写出a、b、c的值，并补全条形统计图；
（2）请问这组数据的中位数在哪一个年龄段中？
（3）在五位36岁的获奖者中有两位美国人，一位法国人和两位俄罗斯人．请用画树形图或列表的方法求出“从五位36岁的获奖者中随机抽出两人，刚好是不同国籍的人”（记作事件A）的概率．

优质解答

（1）由表格可知：当频数为1时，频率为0.025，所以总人数=1÷0.025=40（人）；
所以a=40×0.175=7（人），b=40-1-2-7-5-6-7=12（人），c=6（人），
统计图补全如下：

（2）因为总人数为40人所以中位数在第四组，即35≤x＜37；

（3）设两个美国人代号为1，1，两个俄罗斯人为3，4，一个法国人为2，画树状图得：

∵共有20种等可能的结果，刚好是不同国籍的人有16种情况，
∴P（A）=

16

20

=

4

5

．（1）由表格可知：当频数为1时，频率为0.025，所以总人数=1÷0.025=40（人）；
所以a=40×0.175=7（人），b=40-1-2-7-5-6-7=12（人），c=6（人），
统计图补全如下：

（2）因为总人数为40人所以中位数在第四组，即35≤x＜37；

（3）设两个美国人代号为1，1，两个俄罗斯人为3，4，一个法国人为2，画树状图得：

∵共有20种等可能的结果，刚好是不同国籍的人有16种情况，
∴P（A）=

16

20

=

4

5

．