(1)在区间(0,1)内任选一个数a,求能使方程x2+2ax+12=0有两个不相等的实根的概率;(2)某校规定周末18:30开始考勤,假设该校学生小张与小王在18:00-18:25之间到校,且每人在该时间段的任何时刻到校是等可能的,求小张与小王到校时间相差5分钟之内的概率.
2019-05-28
(1)在区间(0,1)内任选一个数a,求能使方程x2+2ax+=0有两个不相等的实根的概率;
(2)某校规定周末18:30开始考勤,假设该校学生小张与小王在18:00-18:25之间到校,且每人在该时间段的任何时刻到校是等可能的,求小张与小王到校时间相差5分钟之内的概率.
优质解答
(1)要使方程x2+2ax+=0有两个不相等的实根,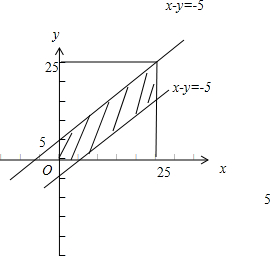
则有△=(2a)2-4×=4a2-2>0,
必须有a2>,
所以a>,由几何概率的定义知所求概率:
p==1-.
(2)设18:00为0时刻,小张、小王到校的时刻分别为x,y,
则,
作出可行域如图,
∴小张与小王到校时间相差5分钟之内的概率:
p=1-×=.
(1)要使方程x2+2ax+=0有两个不相等的实根,
则有△=(2a)2-4×=4a2-2>0,
必须有a2>,
所以a>,由几何概率的定义知所求概率:
p==1-.
(2)设18:00为0时刻,小张、小王到校的时刻分别为x,y,
则,
作出可行域如图,
∴小张与小王到校时间相差5分钟之内的概率:
p=1-×=.



