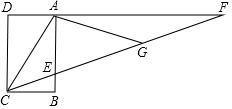
“三等分一个任意角”是数学史上一个著名问题，今天人们已经知道，仅用圆规直尺是不可能做出的．在探索中，有人曾利用过如图所示的图形，其中，ABCD是长方形（AD∥CB），F是DA延长线上一点，G 是CF上一点，并且∠ACG=∠AGC，∠GAF=∠F，你能证明∠ECB=13∠ACB吗？

2019-05-07

“三等分一个任意角”是数学史上一个著名问题，今天人们已经知道，仅用圆规直尺是不可能做出的．在探索中，有人曾利用过如图所示的图形，其中，ABCD是长方形（AD∥CB），F是DA延长线上一点，G 是CF上一点，并且∠ACG=∠AGC，∠GAF=∠F，你能证明∠ECB=

1

3

∠ACB吗？

优质解答

证明：∵四边形ABCD是矩形，
∴AD∥BC，
∴∠F=∠ECB，
∴∠ACG=∠AGC=∠GAF+∠F=2∠F
=2∠ECB，
∴∠ACB=∠ACG+∠ECB=3∠ECB，
∴∠ECB=

1

3

∠ACB．证明：∵四边形ABCD是矩形，
∴AD∥BC，
∴∠F=∠ECB，
∴∠ACG=∠AGC=∠GAF+∠F=2∠F
=2∠ECB，
∴∠ACB=∠ACG+∠ECB=3∠ECB，
∴∠ECB=

1

3

∠ACB．