联想三角形外心的概念,我们可引入如下概念.定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.举例:如图1,若PA=PB,则点P为△ABC的准外心.应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD=12AB,求∠APB的度数.探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长.
2019-06-02
联想三角形外心的概念,我们可引入如下概念.
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
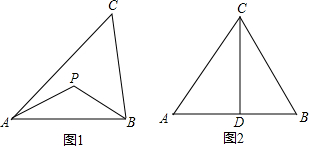
举例:如图1,若PA=PB,则点P为△ABC的准外心.
应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD=AB,求∠APB的度数.
探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长.
优质解答
应用:①若PB=PC,连接PB,则∠PCB=∠PBC,
∵CD为等边三角形的高,
∴AD=BD,∠PCB=30°,
∴∠PBD=∠PBC=30°,
∴PD=DB=AB,
与已知PD=AB矛盾,∴PB≠PC,
②若PA=PC,连接PA,同理可得PA≠PC,
③若PA=PB,由PD=AB,得PD=BD,
∴∠APD=45°,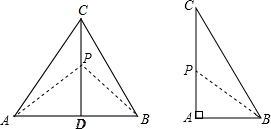
故∠APB=90°;
探究:∵BC=5,AB=3,
∴AC===4,
①若PB=PC,设PA=x,则x2+32=(4-x)2,
∴x=,即PA=,
②若PA=PC,则PA=2,
③若PA=PB,由图知,在Rt△PAB中,不可能.
故PA=2或.
应用:①若PB=PC,连接PB,则∠PCB=∠PBC,
∵CD为等边三角形的高,
∴AD=BD,∠PCB=30°,
∴∠PBD=∠PBC=30°,
∴PD=DB=AB,
与已知PD=AB矛盾,∴PB≠PC,
②若PA=PC,连接PA,同理可得PA≠PC,
③若PA=PB,由PD=AB,得PD=BD,
∴∠APD=45°,
故∠APB=90°;
探究:∵BC=5,AB=3,
∴AC===4,
①若PB=PC,设PA=x,则x2+32=(4-x)2,
∴x=,即PA=,
②若PA=PC,则PA=2,
③若PA=PB,由图知,在Rt△PAB中,不可能.
故PA=2或.
相关问答
- 3把钥匙3把锁.请问至少试多少次才能把3把
- 理念及数学题 一项工程,甲单干60天完成,
- 1加2乘3等于几?1加2乘3计算器上时等于
- 《数学的观念、思想和方法》论述题两道.1.
- 求一数学理念,也就是作为一名数学教师为教学
- 英语翻译模拟电路,电路分析基础,信号与系统
- 这个学期我-共选了12个学分的课程.用英语
- 让讲20分钟的英语课,我们应该怎样讲,讲些
- 人教版高中数学说课稿必修1-5
- 好的高中数学课堂教学模式?
- 高中数学的概念课有哪些
- 建模是数学的核心素养之一,小明在计算
- 解剖两个字有多少人说不出正确的发音,包括每
- 关于春节期间购物的数学小论文,要有表格,不
- 四年级数学小论文开头
- 为什么长方体的公式是长乘宽乘高数学小论文


