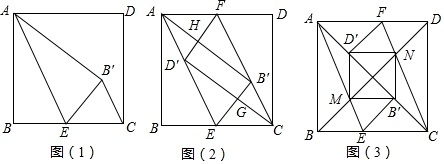
综合与实践:折纸中的数学问题情境:数学活动课上,老师让同学们折叠正方形纸片ABCD进行探究活动,兴趣小组的同学经过动手操作探究,提出了如下两个问题:问题1:如图(1),若点E为BC的中点,设AE将正方形纸片ABCD折叠,点B的对应点为B′,连接B′C,求证:B′C∥AE.问题2:如图(2),若点E,点F分别为边BC,边AD的中点,沿AE、CF将正方形纸片ABCD折叠,点B的对应点为B′,点D的对应点D′,D′F与AB′交于点H,B′E与CD′交于点G,求证:四边形D′GB′H为矩形.(1)解决问题:请你对
2019-06-02
综合与实践:折纸中的数学
问题情境:数学活动课上,老师让同学们折叠正方形纸片ABCD进行探究活动,兴趣小组的同学经过动手操作探究,提出了如下两个问题:
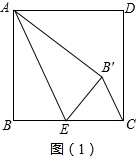
问题1:如图(1),若点E为BC的中点,设AE将正方形纸片ABCD折叠,点B的对应点为B′,连接B′C,求证:B′C∥AE.
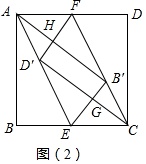
问题2:如图(2),若点E,点F分别为边BC,边AD的中点,沿AE、CF将正方形纸片ABCD折叠,点B的对应点为B′,点D的对应点D′,D′F与AB′交于点H,B′E与CD′交于点G,求证:四边形D′GB′H为矩形.
(1)解决问题:请你对兴趣小组提出的两个问题进行证明.
(2)拓展探究:解决完兴趣小组提出的两个问题后,实践小组的同学们进行如下实践操作:
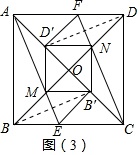
如图(3),点E,点F分别为BC、AD上的点,将正方形纸片沿AE、CF折叠,使得点B落在对角线上的点B′处,点D落在对角线AC上的点D′处,AE与对角线BD的交点为M,CF与对角线BD的交点为N,分别连接MB′,B′N,D′N,D′M.他们认为四边形MB′ND′为正方形.
实践小组的同学们发现的结论是否正确?请你说明理由.
问题情境:数学活动课上,老师让同学们折叠正方形纸片ABCD进行探究活动,兴趣小组的同学经过动手操作探究,提出了如下两个问题:
问题1:如图(1),若点E为BC的中点,设AE将正方形纸片ABCD折叠,点B的对应点为B′,连接B′C,求证:B′C∥AE.
问题2:如图(2),若点E,点F分别为边BC,边AD的中点,沿AE、CF将正方形纸片ABCD折叠,点B的对应点为B′,点D的对应点D′,D′F与AB′交于点H,B′E与CD′交于点G,求证:四边形D′GB′H为矩形.
(1)解决问题:请你对兴趣小组提出的两个问题进行证明.
(2)拓展探究:解决完兴趣小组提出的两个问题后,实践小组的同学们进行如下实践操作:
如图(3),点E,点F分别为BC、AD上的点,将正方形纸片沿AE、CF折叠,使得点B落在对角线上的点B′处,点D落在对角线AC上的点D′处,AE与对角线BD的交点为M,CF与对角线BD的交点为N,分别连接MB′,B′N,D′N,D′M.他们认为四边形MB′ND′为正方形.
实践小组的同学们发现的结论是否正确?请你说明理由.