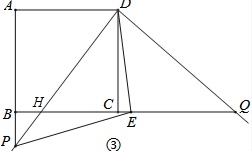
数学兴趣小组开展了一次课外活动,过程如下:如图①,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合,三角板的一边交AB于点P,另一边交BC的延长线于点Q.(1)求证:AP=CQ;(2)如图②,小明在图①的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并证明.(3)如图③,固定三角板直角顶点在D点不动,转到三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC的延长线
2019-06-02
数学兴趣小组开展了一次课外活动,过程如下:
如图①,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合,三角板的一边交AB于点P,另一边交BC的延长线于点Q.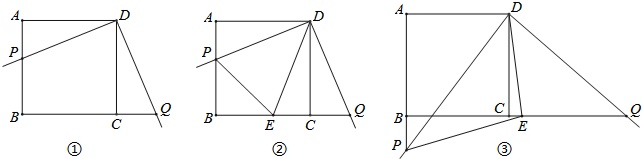
(1)求证:AP=CQ;
(2)如图②,小明在图①的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并证明.
(3)如图③,固定三角板直角顶点在D点不动,转到三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC的延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEQ的面积.
如图①,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合,三角板的一边交AB于点P,另一边交BC的延长线于点Q.

(1)求证:AP=CQ;
(2)如图②,小明在图①的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并证明.
(3)如图③,固定三角板直角顶点在D点不动,转到三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC的延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEQ的面积.