能的转化与守恒是自然界普遍存在的规律，如：电源给电容器的充电过程可以等效为将电荷逐个从原本电中性的两极板中的一个极板移到另一个极板的过程．在移动过程中克服电场力做功，电源的电能转化为电容器的电场能．实验表明：电容器两极间的电压与电容器所带电量如图1所示．（1）对于直线运动，教科书中讲解了由v-t图象求位移的方法．请你借鉴此方法，根据图示的Q-U图象，若电容器电容为C，两极板间电压为U，求电容器所储存的电场能．（2）如图2所示，平行金属框架竖直放置在绝缘地面上．框架上端接有一电容为C的电容器．框架上一质量为

2019-06-26

下载本文

能的转化与守恒是自然界普遍存在的规律，如：电源给电容器的充电过程可以等效为将电荷逐个从原本电中性的两极板中的一个极板移到另一个极板的过程．在移动过程中克服电场力做功，电源的电能转化为电容器的电场能．实验表明：电容器两极间的电压与电容器所带电量如图1所示．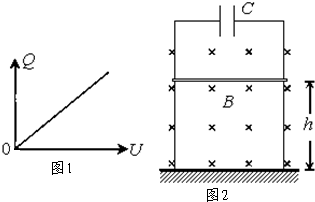

（1）对于直线运动，教科书中讲解了由v-t图象求位移的方法．请你借鉴此方法，根据图示的Q-U图象，若电容器电容为C，两极板间电压为U，求电容器所储存的电场能．
（2）如图2所示，平行金属框架竖直放置在绝缘地面上．框架上端接有一电容为C的电容器．框架上一质量为m、长为L的金属棒平行于地面放置，离地面的高度为h．磁感应强度为B的匀强磁场与框架平面相垂直．现将金属棒由静止开始释放，金属棒下滑过程中与框架接触良好且无摩擦．开始时电容器不带电，不计各处电阻．求：
a．金属棒落地时的速度大小
b．金属棒从静止释放到落到地面的时间．

优质解答

（1）由功能关系分析可知克服电场力做的功等于产生的电场能．
根据速度-时间图象围成的面积代表位移，可知在Q-U图象中，图象所围成的面积为

1

2

QU，也就是克服电场力所做的功．
即为：W=

1

2

QU
又有电容定义式为：C=

Q

U

两式联立得：W=

1

2

CU²，
所以电容器储存的电场能为：E_e=

1

2

CU²，
（2）a、设导体棒落地的速度为v，此时导体棒切割磁感线产生感应电动势，
感应电动势大小为：E=BLv
电容器储存的电场能为：E_e=

1

2

C（BLv）²，
由动能定理得：mgh=

1

2

mv²+E_e
解得：v=

2mgh

m+CB2L2

b、导体棒下落过程中受安培力和重力，由动量定理可知：
mgt-F_安t=m△v
又F_安=BIL
Q=It
Q=CU
△v=v-0
由以上几式解得：t＝

2h(m+CB2L2)

mg

．
答：（1）电容器所储存的电场能为

1

2

CU²．
（2）a．金属棒落地时的速度大小为

2mgh

m+CB2L2

．
b．金属棒从静止释放到落到地面的时间为

2h(m+CB2L2)

mg

．（1）由功能关系分析可知克服电场力做的功等于产生的电场能．
根据速度-时间图象围成的面积代表位移，可知在Q-U图象中，图象所围成的面积为

1

2

QU，也就是克服电场力所做的功．
即为：W=

1

2

QU
又有电容定义式为：C=

Q

U

两式联立得：W=

1

2

CU²，
所以电容器储存的电场能为：E_e=

1

2

CU²，
（2）a、设导体棒落地的速度为v，此时导体棒切割磁感线产生感应电动势，
感应电动势大小为：E=BLv
电容器储存的电场能为：E_e=

1

2

C（BLv）²，
由动能定理得：mgh=

1

2

mv²+E_e
解得：v=

2mgh

m+CB2L2

b、导体棒下落过程中受安培力和重力，由动量定理可知：
mgt-F_安t=m△v
又F_安=BIL
Q=It
Q=CU
△v=v-0
由以上几式解得：t＝

2h(m+CB2L2)

mg

．
答：（1）电容器所储存的电场能为

1

2

CU²．
（2）a．金属棒落地时的速度大小为

2mgh

m+CB2L2

．
b．金属棒从静止释放到落到地面的时间为

2h(m+CB2L2)

mg

．