精选问答
已知0≤a＜2，0≤b＜4，为估计在a＞1的条件下，函数f（x）=x2+2ax+b有两相异零点的概率P．用计算机产生了[{0，1}）内的两组随机数a1，b1各2400个，并组成了2400个有序数对（a1，b1），统计这2400个有序数对后得到2×2列联表的部分数据如下表：则数据表中数据计算出的概率P的估计值为（　　）A．1348B．1124C．1960D．712

2019-05-30

已知0≤a＜2，0≤b＜4，为估计在a＞1的条件下，函数f（x）=x2+2ax+b有两相异零点的概率P．用计算机产生了[{0，1}）内的两组随机数a1，b1各2400个，并组成了2400个有序数对（a1，b1），统计这2400个有序数对后得到2×2列联表的部分数据如下表：

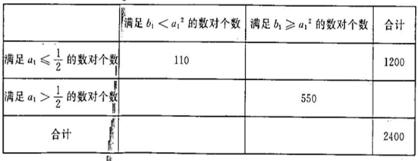
则数据表中数据计算出的概率P的估计值为（　　）

A．
13
48

B．
11
24

C．
19
60

D．
7
12
优质解答
要使得函数f（x）=x2+2ax+b有两相异零点，
4a2-4b＞0，
∴a2＞b，
条件中所给的共有2400对有序数对，
在这些有序数对中，使得函数有两个相异的零点，
共有110+（1200-550）=760，
∴数据表中数据计算出的概率P的估计值是
760
2400
=
19
60
．
故选C 要使得函数f（x）=x2+2ax+b有两相异零点，
4a2-4b＞0，
∴a2＞b，
条件中所给的共有2400对有序数对，
在这些有序数对中，使得函数有两个相异的零点，
共有110+（1200-550）=760，
∴数据表中数据计算出的概率P的估计值是
760
2400
=
19
60
．
故选C
相关问答