优质解答
思路:
有一个定理在这里要用到的:
若长为|a|,|b|的线段可以用几何方法做出来,那么长为|c|的线段也能用几何方法做出的,
其中c是方程x^2+ax+b=0的实根.
上面的定理实际上就是在有线段长度|a|和|b|的时候,做出长为sqrt(a^2-4b)的线段.
(这一步,大家会画吧?)
而要在一个单位圆中做出正十七边形,主要就是做出长度是cos(2pai/17)的线段.
下面我把当年高斯证明可以做出cos(2pai/17)的证明给出,同时也就给出了具体的做法.
设a=2[cos(2pai/17)+cos(4pai/17)+cos(8pai/17)+cos(16pai/17)]>0
a1=2[cos(6pai/17)+cos(10pai/17)+cos(12pai/17)+cos(14pai/17)]<0
则有a+a1=-1,a*a1=-4,即a,a1是方程x^2+x-4=0的根,所以长为|a|和|a1|的线段可以做出.
令b=2[cos(2pai/17)+cos(8pai/17)]>0 b1=2[cos(4pai/17)+cos(16pai/17)]<0
c=2[cos(6pai/17)+cos(10pai/17)]>0 c1=2[cos(12pai/17)+cos(14pai/17)]<0
则有b+b1=a b*b1=-1 c+c1=a1 c*c1=-1
同样道理,长度是|b|,|b1|,|c|,|c1|的线段都可以做出来的.
再有2cos(2pai/17)+2cos(8pai/17)=b [2cos(2pai/17)]*[2cos(8pai/17)]=c
这样,2cos(2pai/17)是方程x^2-bx+c=0较大的实根,
显然也可以做出来,并且作图的方法上面已经给出来了
解法1:
①
给一圆O,作两垂直的半径OA、OB,
作C点使OC=1/4OB,
作D点使∠OCD=1/4∠OCA 作AO延长线上E点使得∠DCE=45度
②
作AE中点M,并以M为圆心作一圆过A点,此圆交OB于F点,
再以D为圆心,作一圆过F点,此圆交直线OA于G4和G6两点.
③
过G4作OA垂直线交圆O于P4,
过G6作OA垂直线交圆O于P6,
则以圆O为基准圆,A为正十七边形之第一顶点P4为第四顶点,P6为第六顶点.
以1/2弧P4P6为半径,即可在此圆上截出正十七边形的所有顶点.
解法2:
在与圆O的直径AB垂直的半径OC上,作出OC的中点D,
在OB上作一点E,使OE等于半径的1/8;
以E为圆心,ED长为半径作弧,与OA、OB分别交于F、G;
以F为圆心,FD长为半径作弧,交OA延长线于H,
以G为圆心,GD长为半径作弧,交OA于I;
作OB中点J,以线段IJ为直径作圆,交OC于 K;
过K作AB的平行线,与以线段OH为直径的圆交于远端L,
过L作OC的平行线,与圆O交于M.
弧AM就是圆O的1/17.
依次连结各点就行了
 思路:
思路:
有一个定理在这里要用到的:
若长为|a|,|b|的线段可以用几何方法做出来,那么长为|c|的线段也能用几何方法做出的,
其中c是方程x^2+ax+b=0的实根.
上面的定理实际上就是在有线段长度|a|和|b|的时候,做出长为sqrt(a^2-4b)的线段.
(这一步,大家会画吧?)
而要在一个单位圆中做出正十七边形,主要就是做出长度是cos(2pai/17)的线段.
下面我把当年高斯证明可以做出cos(2pai/17)的证明给出,同时也就给出了具体的做法.
设a=2[cos(2pai/17)+cos(4pai/17)+cos(8pai/17)+cos(16pai/17)]>0
a1=2[cos(6pai/17)+cos(10pai/17)+cos(12pai/17)+cos(14pai/17)]<0
则有a+a1=-1,a*a1=-4,即a,a1是方程x^2+x-4=0的根,所以长为|a|和|a1|的线段可以做出.
令b=2[cos(2pai/17)+cos(8pai/17)]>0 b1=2[cos(4pai/17)+cos(16pai/17)]<0
c=2[cos(6pai/17)+cos(10pai/17)]>0 c1=2[cos(12pai/17)+cos(14pai/17)]<0
则有b+b1=a b*b1=-1 c+c1=a1 c*c1=-1
同样道理,长度是|b|,|b1|,|c|,|c1|的线段都可以做出来的.
再有2cos(2pai/17)+2cos(8pai/17)=b [2cos(2pai/17)]*[2cos(8pai/17)]=c
这样,2cos(2pai/17)是方程x^2-bx+c=0较大的实根,
显然也可以做出来,并且作图的方法上面已经给出来了
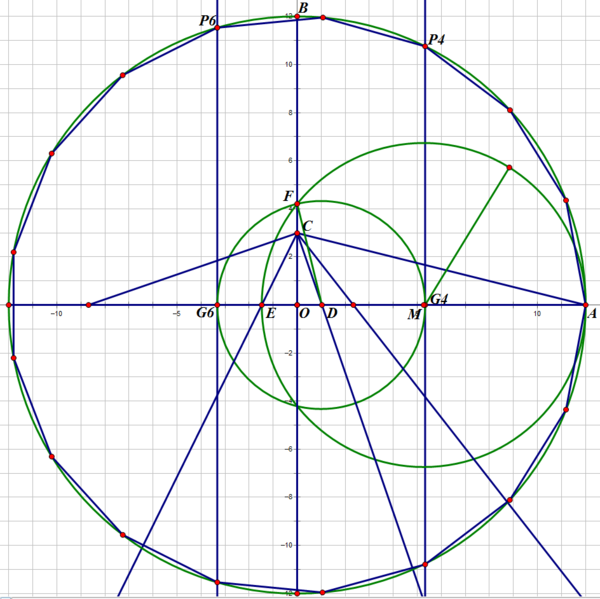
解法1:
①
给一圆O,作两垂直的半径OA、OB,
作C点使OC=1/4OB,
作D点使∠OCD=1/4∠OCA 作AO延长线上E点使得∠DCE=45度
②
作AE中点M,并以M为圆心作一圆过A点,此圆交OB于F点,
再以D为圆心,作一圆过F点,此圆交直线OA于G4和G6两点.
③
过G4作OA垂直线交圆O于P4,
过G6作OA垂直线交圆O于P6,
则以圆O为基准圆,A为正十七边形之第一顶点P4为第四顶点,P6为第六顶点.
以1/2弧P4P6为半径,即可在此圆上截出正十七边形的所有顶点.
解法2:
在与圆O的直径AB垂直的半径OC上,作出OC的中点D,
在OB上作一点E,使OE等于半径的1/8;
以E为圆心,ED长为半径作弧,与OA、OB分别交于F、G;
以F为圆心,FD长为半径作弧,交OA延长线于H,
以G为圆心,GD长为半径作弧,交OA于I;
作OB中点J,以线段IJ为直径作圆,交OC于 K;
过K作AB的平行线,与以线段OH为直径的圆交于远端L,
过L作OC的平行线,与圆O交于M.
弧AM就是圆O的1/17.
依次连结各点就行了

有一个定理在这里要用到的:
若长为|a|,|b|的线段可以用几何方法做出来,那么长为|c|的线段也能用几何方法做出的,
其中c是方程x^2+ax+b=0的实根.
上面的定理实际上就是在有线段长度|a|和|b|的时候,做出长为sqrt(a^2-4b)的线段.
(这一步,大家会画吧?)
而要在一个单位圆中做出正十七边形,主要就是做出长度是cos(2pai/17)的线段.
下面我把当年高斯证明可以做出cos(2pai/17)的证明给出,同时也就给出了具体的做法.
设a=2[cos(2pai/17)+cos(4pai/17)+cos(8pai/17)+cos(16pai/17)]>0
a1=2[cos(6pai/17)+cos(10pai/17)+cos(12pai/17)+cos(14pai/17)]<0
则有a+a1=-1,a*a1=-4,即a,a1是方程x^2+x-4=0的根,所以长为|a|和|a1|的线段可以做出.
令b=2[cos(2pai/17)+cos(8pai/17)]>0 b1=2[cos(4pai/17)+cos(16pai/17)]<0
c=2[cos(6pai/17)+cos(10pai/17)]>0 c1=2[cos(12pai/17)+cos(14pai/17)]<0
则有b+b1=a b*b1=-1 c+c1=a1 c*c1=-1
同样道理,长度是|b|,|b1|,|c|,|c1|的线段都可以做出来的.
再有2cos(2pai/17)+2cos(8pai/17)=b [2cos(2pai/17)]*[2cos(8pai/17)]=c
这样,2cos(2pai/17)是方程x^2-bx+c=0较大的实根,
显然也可以做出来,并且作图的方法上面已经给出来了
解法1:
①
给一圆O,作两垂直的半径OA、OB,
作C点使OC=1/4OB,
作D点使∠OCD=1/4∠OCA 作AO延长线上E点使得∠DCE=45度
②
作AE中点M,并以M为圆心作一圆过A点,此圆交OB于F点,
再以D为圆心,作一圆过F点,此圆交直线OA于G4和G6两点.
③
过G4作OA垂直线交圆O于P4,
过G6作OA垂直线交圆O于P6,
则以圆O为基准圆,A为正十七边形之第一顶点P4为第四顶点,P6为第六顶点.
以1/2弧P4P6为半径,即可在此圆上截出正十七边形的所有顶点.
解法2:
在与圆O的直径AB垂直的半径OC上,作出OC的中点D,
在OB上作一点E,使OE等于半径的1/8;
以E为圆心,ED长为半径作弧,与OA、OB分别交于F、G;
以F为圆心,FD长为半径作弧,交OA延长线于H,
以G为圆心,GD长为半径作弧,交OA于I;
作OB中点J,以线段IJ为直径作圆,交OC于 K;
过K作AB的平行线,与以线段OH为直径的圆交于远端L,
过L作OC的平行线,与圆O交于M.
弧AM就是圆O的1/17.
依次连结各点就行了
 思路:
思路:有一个定理在这里要用到的:
若长为|a|,|b|的线段可以用几何方法做出来,那么长为|c|的线段也能用几何方法做出的,
其中c是方程x^2+ax+b=0的实根.
上面的定理实际上就是在有线段长度|a|和|b|的时候,做出长为sqrt(a^2-4b)的线段.
(这一步,大家会画吧?)
而要在一个单位圆中做出正十七边形,主要就是做出长度是cos(2pai/17)的线段.
下面我把当年高斯证明可以做出cos(2pai/17)的证明给出,同时也就给出了具体的做法.
设a=2[cos(2pai/17)+cos(4pai/17)+cos(8pai/17)+cos(16pai/17)]>0
a1=2[cos(6pai/17)+cos(10pai/17)+cos(12pai/17)+cos(14pai/17)]<0
则有a+a1=-1,a*a1=-4,即a,a1是方程x^2+x-4=0的根,所以长为|a|和|a1|的线段可以做出.
令b=2[cos(2pai/17)+cos(8pai/17)]>0 b1=2[cos(4pai/17)+cos(16pai/17)]<0
c=2[cos(6pai/17)+cos(10pai/17)]>0 c1=2[cos(12pai/17)+cos(14pai/17)]<0
则有b+b1=a b*b1=-1 c+c1=a1 c*c1=-1
同样道理,长度是|b|,|b1|,|c|,|c1|的线段都可以做出来的.
再有2cos(2pai/17)+2cos(8pai/17)=b [2cos(2pai/17)]*[2cos(8pai/17)]=c
这样,2cos(2pai/17)是方程x^2-bx+c=0较大的实根,
显然也可以做出来,并且作图的方法上面已经给出来了
解法1:
①
给一圆O,作两垂直的半径OA、OB,
作C点使OC=1/4OB,
作D点使∠OCD=1/4∠OCA 作AO延长线上E点使得∠DCE=45度
②
作AE中点M,并以M为圆心作一圆过A点,此圆交OB于F点,
再以D为圆心,作一圆过F点,此圆交直线OA于G4和G6两点.
③
过G4作OA垂直线交圆O于P4,
过G6作OA垂直线交圆O于P6,
则以圆O为基准圆,A为正十七边形之第一顶点P4为第四顶点,P6为第六顶点.
以1/2弧P4P6为半径,即可在此圆上截出正十七边形的所有顶点.
解法2:
在与圆O的直径AB垂直的半径OC上,作出OC的中点D,
在OB上作一点E,使OE等于半径的1/8;
以E为圆心,ED长为半径作弧,与OA、OB分别交于F、G;
以F为圆心,FD长为半径作弧,交OA延长线于H,
以G为圆心,GD长为半径作弧,交OA于I;
作OB中点J,以线段IJ为直径作圆,交OC于 K;
过K作AB的平行线,与以线段OH为直径的圆交于远端L,
过L作OC的平行线,与圆O交于M.
弧AM就是圆O的1/17.
依次连结各点就行了
