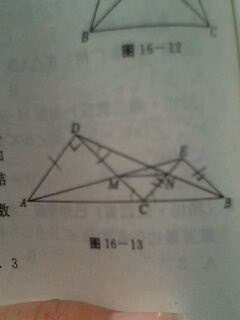
一道初中数学题如图,已知C是线段AB上任意一点(端点除外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角三角形ACD和等腰直角三角形BCE,连结AE交CD于点M,连结BD交CE于点N,证明以下三个结论:1.MN//AB 2.1/MN=1/AC+1/BC 3.MN小于等于四分之一倍的AB
2019-06-01
一道初中数学题
如图,已知C是线段AB上任意一点(端点除外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角三角形ACD和等腰直角三角形BCE,连结AE交CD于点M,连结BD交CE于点N,证明以下三个结论:1.MN//AB
2.1/MN=1/AC+1/BC
3.MN小于等于四分之一倍的AB
如图,已知C是线段AB上任意一点(端点除外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角三角形ACD和等腰直角三角形BCE,连结AE交CD于点M,连结BD交CE于点N,证明以下三个结论:1.MN//AB
2.1/MN=1/AC+1/BC
3.MN小于等于四分之一倍的AB