联想三角形内心的概念,我们可引入如下概念.定义:到三角形的两边距离相等的点,叫做此三角形的准内心.举例:如图1,若PD=PE,则点P为△ABC的准内心.应用:如图2,BF为等边三角形的角平分线,准内心P在BF上,且PF=12BP,求证:点P是△ABC的内心.探究:已知△ABC为直角三角形,∠C=90°,准内心P在AC上,若PC=12AP,求∠A的度数.
2019-06-02
联想三角形内心的概念,我们可引入如下概念.
定义:到三角形的两边距离相等的点,叫做此三角形的准内心.
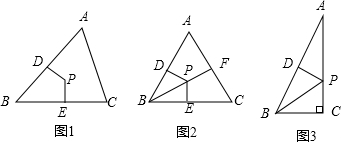
举例:如图1,若PD=PE,则点P为△ABC的准内心.
应用:如图2,BF为等边三角形的角平分线,准内心P在BF上,且PF=
BP,求证:点P是△ABC的内心.
探究:已知△ABC为直角三角形,∠C=90°,准内心P在AC上,若PC=
AP,求∠A的度数.
定义:到三角形的两边距离相等的点,叫做此三角形的准内心.
举例:如图1,若PD=PE,则点P为△ABC的准内心.
应用:如图2,BF为等边三角形的角平分线,准内心P在BF上,且PF=
| 1 |
| 2 |
探究:已知△ABC为直角三角形,∠C=90°,准内心P在AC上,若PC=
| 1 |
| 2 |
