数学兴趣小组研究某型号冷柜温度的变化情况，发现该冷柜的工作过程是：当温度达到设定温度-20℃时，制冷停止，此后冷柜中的温度开始逐渐上升，当上升到-4℃时，制冷开始，温度开始逐渐下降，当冷柜自动制冷至-20℃时，制冷再次停止，…，按照以上方式循环进行．同学们记录了44min内15个时间点冷柜中的温度y（℃）随时间x（min）的变化情况，制成下表：时间x/min … 4 8 10 16 20 21 22 23 24 2

2019-06-02

下载本文

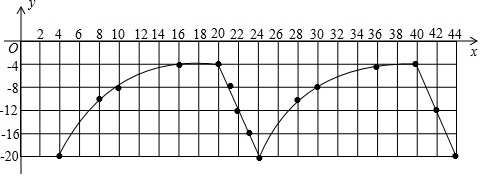
数学兴趣小组研究某型号冷柜温度的变化情况，发现该冷柜的工作过程是：当温度达到设定温度-20℃时，制冷停止，此后冷柜中的温度开始逐渐上升，当上升到-4℃时，制冷开始，温度开始逐渐下降，当冷柜自动制冷至-20℃时，制冷再次停止，…，按照以上方式循环进行．
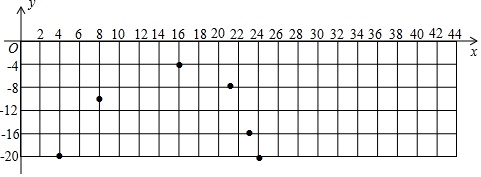
同学们记录了44min内15个时间点冷柜中的温度y（℃）随时间x（min）的变化情况，制成下表：

时间x/min	…	4	8	10	16	20	21	22	23	24	28	30	36	40	42	44	…
温度y/℃	…	-20	-10	-8	-5	-4	-8	-12	-16	-20	-10	-8	-5	-4	a	-20	…

（1）通过分析发现，冷柜中的温度y是时间x的函数．
①当4≤x<20时，写出一个符合表中数据的函数解析式___；
②当20≤x<24时，写出一个符合表中数据的函数解析式___；
（2）a的值为___；
（3）如图，在直角坐标系中，已描出了上表中部分数据对应的点，请描出剩余数据对应的点，并画出当4≤x≤44时温度y随时间x变化的函数图象．作业帮

优质解答

（1）①∵4×（-20）=-80，8×（-10）=-80，10×（-8）=-80，16×（-5）=-80，20×（-4）=-80，
∴当4≤x<20时，y=-

80

x

．
故答案为：y=-

80

x

．
②当20≤x<24时，设y关于x的函数解析式为y=kx+b，
将（20，-4）、（21，-8）代入y=kx+b中，

20k+b=-4

21k+b=-8

，解得：

k=-4

b=76

，
∴此时y=-4x+76．作业帮

当x=22时，y=-4x+76=-12，
当x=23时，y=-4x+76=-16，
当x=24时，y=-4x+76=-20．
∴当20≤x<24时，y=-4x+76．
故答案为：y=-4x+76．
（2）观察表格，可知该冷柜的工作周期为20分钟，
∴当x=42时，与x=22时，y值相同，
∴a=-12．
故答案为：-12．
（3）描点、连线，画出函数图象，如图所示．（1）①∵4×（-20）=-80，8×（-10）=-80，10×（-8）=-80，16×（-5）=-80，20×（-4）=-80，
∴当4≤x<20时，y=-

80

x