物理
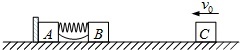
如图所示，光滑水平面上放着质量都为m的物块A和B，A紧靠着固定的竖直挡板，A、B 间夹一个被压缩的轻弹簧（弹簧与A、B均不拴接），用手挡住B不动，此时弹簧弹性势能为92mv02．在A、B间系一轻质细绳，细绳的长略大于弹簧的自然长度．放手后绳在短暂时间内被拉断，之后B继续向右运动，一段时间后与向左匀速运动、速度为v0的物块C发生碰撞，碰后B、C立刻形成粘合体并停止运动，C的质量为2m．求：（ⅰ） B、C相撞前一瞬间B的速度大小；（ⅱ）绳被拉断过程中，绳对A所做的功W．

2019-06-25

如图所示，光滑水平面上放着质量都为m的物块A和B，A紧靠着固定的竖直挡板，A、B 间夹一个被压缩的轻弹簧（弹簧与A、B均不拴接），用手挡住B不动，此时弹簧弹性势能为
9
2
mv02．在A、B间系一轻质细绳，细绳的长略大于弹簧的自然长度．放手后绳在短暂时间内被拉断，之后B继续向右运动，一段时间后与向左匀速运动、速度为v0的物块C发生碰撞，碰后B、C立刻形成粘合体并停止运动，C的质量为2m．求：
（ⅰ） B、C相撞前一瞬间B的速度大小；
（ⅱ）绳被拉断过程中，绳对A所做的功W．
作业帮
优质解答
（ⅰ）B与C碰撞过程中，动量守恒，以B的初速度方向为正，根据动量守恒定律得：
mvB-2mv0=0，
解得：vB=2v0
（ⅱ）弹簧恢复原长时，弹性势能全部转化为物块B的动能，则
EP=
1
2
mv
2
B0

解得：vB0=3v0，
绳子拉断过程，A、B系统动量守恒，以B的初速度方向为正，根据动量守恒定律得：
mvB0=mvB+mvA  
解得：vA=v0
由动能定理可得，绳对A所做的功W=
1
2
mv
2
A
=
1
2
mv
2
0

答：（ⅰ） B、C相撞前一瞬间B的速度大小为2v0；
（ⅱ）绳被拉断过程中，绳对A所做的功W为
1
2
mv
2
0
． （ⅰ）B与C碰撞过程中，动量守恒，以B的初速度方向为正，根据动量守恒定律得：
mvB-2mv0=0，
解得：vB=2v0
（ⅱ）弹簧恢复原长时，弹性势能全部转化为物块B的动能，则
EP=
1
2
mv
2
B0

解得：vB0=3v0，
绳子拉断过程，A、B系统动量守恒，以B的初速度方向为正，根据动量守恒定律得：
mvB0=mvB+mvA  
解得：vA=v0
由动能定理可得，绳对A所做的功W=
1
2
mv
2
A
=
1
2
mv
2
0

答：（ⅰ） B、C相撞前一瞬间B的速度大小为2v0；
（ⅱ）绳被拉断过程中，绳对A所做的功W为
1
2
mv
2
0
．
相关问答