数学
某校九年级数学兴趣小组的活动课题是“测量物体高度”．小组成员小明与小红分别采用不同的方案测量同一个底面为圆形的古塔高度，以下是他们研究报告的部分记录内容： 课题：测量古塔的高度 小明的研究报告 小红的研究报告 图示 测量方案与测量数据 　  用距离地面高度为1.6m的测角器测出古塔顶端的仰角为35°，再用皮尺测得测角器所在位置与古塔底部边缘的最短距离为30m． 在点A用距离地面高度为1.6m的测角器测出

2019-06-02

某校九年级数学兴趣小组的活动课题是“测量物体高度”．小组成员小明与小红分别采用不同的方案测量同一个底面为圆形的古塔高度，以下是他们研究报告的部分记录内容：
课题：测量古塔的高度
小明的研究报告 小红的研究报告
图示 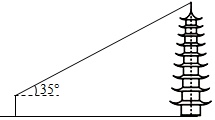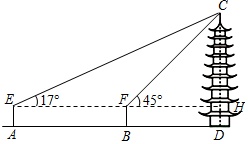作业帮 作业帮
测量方案与测量数据 　  用距离地面高度为1.6m的测角器测出古塔顶端的仰角为35°，再用皮尺测得测角器所在位置与古塔底部边缘的最短距离为30m． 在点A用距离地面高度为1.6m的测角器测出古塔顶端的仰角为17°，然后沿AD方向走58.8m到达点B，测出古塔顶端的仰角为45°．
参考数据 sin35°≈0.57，cos35°≈0.82，tan35°≈0.70 sin17°≈0.29，cos17°≈0.96，tan17°≈0.30，
2
≈1.41
计算古塔高度
（结果精确到0.1m）		 30×tan35°+1.6≈22.6（m）
（1）写出小红研究报告中“计算古塔高度”的解答过程；
（2）数学老师说小红的结果较准确，而小明的结果与古塔的实际高度偏差较大．针对小明的测量方案分析测量发生偏差的原因；
（3）利用小明与小红的测量数据，估算该古塔底面圆直径的长度为___m．
优质解答
（1）设CH=x，
在Rt△CHF中，∵∠CFH=∠FCH=45°，
∴CH=FH=x，
在Rt△CHE中，
∵tan∠CEH=
CH
EH
，
∴
x
x+58.8
=tan17°=0.30，
∴x=25.2，即CH=25.2（m），
∴CD=CH+DH=25.2+1.6=26.8（m），
答：古塔CD的高度为26.8m；

（2）原因：小明测量的只是测角器所在位置与古塔底部边缘的最短距离，不是测量测角器所在位置与底面圆心的最短距离．

（3）∵26.8-22.6=4.2，
∴该古塔底面圆直径的长度=2×4.2=8.4（m）．
故答案为：8.4． （1）设CH=x，
在Rt△CHF中，∵∠CFH=∠FCH=45°，
∴CH=FH=x，
在Rt△CHE中，
∵tan∠CEH=
CH
EH
，
∴
x
x+58.8
=tan17°=0.30，
∴x=25.2，即CH=25.2（m），
∴CD=CH+DH=25.2+1.6=26.8（m），
答：古塔CD的高度为26.8m；

（2）原因：小明测量的只是测角器所在位置与古塔底部边缘的最短距离，不是测量测角器所在位置与底面圆心的最短距离．

（3）∵26.8-22.6=4.2，
∴该古塔底面圆直径的长度=2×4.2=8.4（m）．
故答案为：8.4．
相关问答