(2014•顺德区模拟)如图所示,质量均为M的小车A、B,B车上挂有质量为M4的金属球C,C球相对于B车静止,其悬线长0.4m,若两车以相同的速率1.8m/s在光滑平面上相向运动,相碰后连在一起(碰撞时间很短),则:(1)两车碰撞后瞬间A车、B车、C球的速度各多大?(2)C球向上摆动的最大高度是多少?
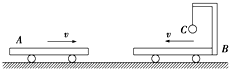 (2014•顺德区模拟)如图所示,质量均为M的小车A、B,B车上挂有质量为
(2014•顺德区模拟)如图所示,质量均为M的小车A、B,B车上挂有质量为
的金属球C,C球相对于B车静止,其悬线长0.4m,若两车以相同的速率1.8m/s在光滑平面上相向运动,相碰后连在一起(碰撞时间很短),则:
(1)两车碰撞后瞬间A车、B车、C球的速度各多大?
(2)C球向上摆动的最大高度是多少?
2019-06-21
 (2014•顺德区模拟)如图所示,质量均为M的小车A、B,B车上挂有质量为
(2014•顺德区模拟)如图所示,质量均为M的小车A、B,B车上挂有质量为| M |
| 4 |
(1)两车碰撞后瞬间A车、B车、C球的速度各多大?
(2)C球向上摆动的最大高度是多少?