(2010•淄博一模)如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC中点,AF=AB=BC=FE=12AD(I)求证:BF⊥DM(Ⅱ)求二面角A-CD-E的余弦值.
2019-04-29
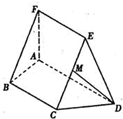 (2010•淄博一模)如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC中点,AF=AB=BC=FE=AD
(2010•淄博一模)如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC中点,AF=AB=BC=FE=AD
(I)求证:BF⊥DM
(Ⅱ)求二面角A-CD-E的余弦值.
优质解答
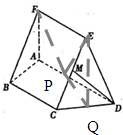 (I)证明:设P为AD的中点,连接EP,PC,
(I)证明:设P为AD的中点,连接EP,PC,
所以由已知,EFAPBC
∴EP=PC,FA∥EP,EC∥BF,AB∥PC…(2分)
又∵FA⊥平面ABCD,
∴EP⊥平面ABCD
因为PC、AD⊂平面ABCD
所以EP⊥PC,EP⊥AD
设FA=a,则EP=PC=PD=a,
∴ED=CD=a…(5分)
∵M为EC的中点,
∴DM⊥CE
∵BF∥EC
∴DM⊥BF.…(6分)
(II)取CD的中点Q,连接PQ,EQ
由(I)知PC=PD,CE=DE
∴PQ⊥CD,EQ⊥CD
∴∠EQP为二面角A-CD-E的平面角…(10分)
由(I)可得,在等边△ECD中EQ=a
在等腰Rt△CPD中,PQ=a
在Rt△EPQ中,cos∠EQP==
故二面角A-CD-E的余弦值为.…(12分)
 (I)证明:设P为AD的中点,连接EP,PC,
(I)证明:设P为AD的中点,连接EP,PC,
所以由已知,EFAPBC
∴EP=PC,FA∥EP,EC∥BF,AB∥PC…(2分)
又∵FA⊥平面ABCD,
∴EP⊥平面ABCD
因为PC、AD⊂平面ABCD
所以EP⊥PC,EP⊥AD
设FA=a,则EP=PC=PD=a,
∴ED=CD=a…(5分)
∵M为EC的中点,
∴DM⊥CE
∵BF∥EC
∴DM⊥BF.…(6分)
(II)取CD的中点Q,连接PQ,EQ
由(I)知PC=PD,CE=DE
∴PQ⊥CD,EQ⊥CD
∴∠EQP为二面角A-CD-E的平面角…(10分)
由(I)可得,在等边△ECD中EQ=a
在等腰Rt△CPD中,PQ=a
在Rt△EPQ中,cos∠EQP==
故二面角A-CD-E的余弦值为.…(12分)
 (2010•淄博一模)如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC中点,AF=AB=BC=FE=
(2010•淄博一模)如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC中点,AF=AB=BC=FE= (2010•淄博一模)如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC中点,AF=AB=BC=FE=
(2010•淄博一模)如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC中点,AF=AB=BC=FE= (I)证明:设P为AD的中点,连接EP,PC,
(I)证明:设P为AD的中点,连接EP,PC,