如图所示，两块相距为d，足够长的金属板A、B平行竖直放置，两板间为匀强电场，电场强度为E，方向水平向右，长为L的绝缘细线一端拴质量为m的带电小球，另一端固定在左板上某点，小球静止时绝缘线与竖直方向的夹角为θ．如突然将细线剪断，问： （1）小球将如何运动？（2）小球经多长时间打到金属板上？
2019-04-19
如图所示，两块相距为d，足够长的金属板A、B平行竖直放置，两板间为匀强电场，电场强度为E，方向水平向右，长为L的绝缘细线一端拴质量为m的带电小球，另一端固定在左板上某点，小球静止时绝缘线与竖直方向的夹角为θ．如突然将细线剪断，问：
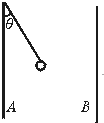
（1）小球将如何运动？
（2）小球经多长时间打到金属板上？
优质解答
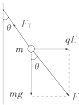（1）小球静止时，受三力：电场力qE、重力mg、线的拉力FT，如图所示．
由平衡条件可以判定，FT和重力mg、电场力qE的合力F是一对平衡力．
剪断线后，线的拉力FT立即消失，小球受重力、电场力的合力仍为恒力F，方向沿线原来方向（即与板成θ角），所以小球将沿线向右下方做初速度为零的匀加速直线运动，直至打到右侧金属板上．
（2）由图可知，小球受到的合外力：F= ①
由牛顿第二定律得：a= …②
打到金属板上前，小球的位移：x=-L …③
由运动公式有：x=at2 …④
②③④联立解得：t=．
答：（1）小球将沿线向右下方做初速度为零的匀加速直线运动，直至打到右侧金属板上．
（2）小球经过时间打到金属板上．
（1）小球静止时，受三力：电场力qE、重力mg、线的拉力FT，如图所示．
由平衡条件可以判定，FT和重力mg、电场力qE的合力F是一对平衡力．
剪断线后，线的拉力FT立即消失，小球受重力、电场力的合力仍为恒力F，方向沿线原来方向（即与板成θ角），所以小球将沿线向右下方做初速度为零的匀加速直线运动，直至打到右侧金属板上．
（2）由图可知，小球受到的合外力：F= ①
由牛顿第二定律得：a= …②
打到金属板上前，小球的位移：x=-L …③
由运动公式有：x=at2 …④
②③④联立解得：t=．
答：（1）小球将沿线向右下方做初速度为零的匀加速直线运动，直至打到右侧金属板上．
（2）小球经过时间打到金属板上．