如图,抛物线y=ax2+bx+c(a、b、c为常数,a≠0)经过点A(-1,0),B(5,-6),C(6,0).(1)求抛物线的解析式;(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;(3)若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.
2019-04-22
如图,抛物线y=ax2+bx+c(a、b、c为常数,a≠0)经过点A(-1,0),B(5,-6),C(6,0).
(1)求抛物线的解析式;
(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.
优质解答
 (1)设y=a(x+1)(x-6)(a≠0),
(1)设y=a(x+1)(x-6)(a≠0),
把B(5,-6)代入:a(5+1)(5-6)=-6,
a=1,
∴y=(x+1)(x-6)=x2-5x-6;
(2)存在,
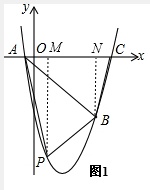
如图1,分别过P、B向x轴作垂线PM和BN,垂足分别为M、N,
设P(m,m2-5m-6),四边形PACB的面积为S,
则PM=-m2+5m+6,AM=m+1,MN=5-m,CN=6-5=1,BN=5,
∴S=S△AMP+S梯形PMNB+S△BNC
=(-m2+5m+6)(m+1)+(6-m2+5m+6)(5-m)+×1×6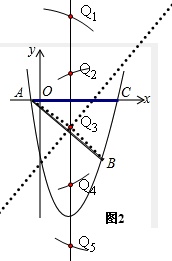
=-3m2+12m+36
=-3(m-2)2+48,
当m=2时,S有最大值为48,这时m2-5m-6=22-5×2-6=-12,
∴P(2,-12),
(3)这样的Q点一共有5个,连接Q3A、Q3B,
y=x2-5x-6=(x-)2-;
因为Q3在对称轴上,所以设Q3(,y),
∵△Q3AB是等腰三角形,且Q3A=Q3B,
由勾股定理得:(+1)2+y2=(-5)2+(y+6)2,
y=-,
∴Q3(,-).
 (1)设y=a(x+1)(x-6)(a≠0),
(1)设y=a(x+1)(x-6)(a≠0),
把B(5,-6)代入:a(5+1)(5-6)=-6,
a=1,
∴y=(x+1)(x-6)=x2-5x-6;
(2)存在,
如图1,分别过P、B向x轴作垂线PM和BN,垂足分别为M、N,
设P(m,m2-5m-6),四边形PACB的面积为S,
则PM=-m2+5m+6,AM=m+1,MN=5-m,CN=6-5=1,BN=5,
∴S=S△AMP+S梯形PMNB+S△BNC
=(-m2+5m+6)(m+1)+(6-m2+5m+6)(5-m)+×1×6
=-3m2+12m+36
=-3(m-2)2+48,
当m=2时,S有最大值为48,这时m2-5m-6=22-5×2-6=-12,
∴P(2,-12),
(3)这样的Q点一共有5个,连接Q3A、Q3B,
y=x2-5x-6=(x-)2-;
因为Q3在对称轴上,所以设Q3(,y),
∵△Q3AB是等腰三角形,且Q3A=Q3B,
由勾股定理得:(+1)2+y2=(-5)2+(y+6)2,
y=-,
∴Q3(,-).
相关问答
- (急!)按规律填数:4,9,(),43,9
- 从4名男生和3名女生中选出3人,分别从事三
- 从4名男生和3名女生中选出3人,分别从事三
- 1.六年级(1)班男生比女生少1/5,男、
- 在北海市创建全国文明城活动中,需要20名志
- 古典概率的计算某班级组织一次活动,现从10
- 1.男生人数占总人数的七分之四,男生人数和
- 1、男的10%和14名女生参加比赛,剩下男
- 1.从甲堆货物中取出1/9给乙堆货物,这时
- 某公司从大学招收毕业生,经过综合测试,录用
- 成都七中学生会经过综合考评,新招了14名男
- 现有7名同学,其中男生4人,女生3人,若从
- 1.李师傅要做600个零件,前面8小时做了
- 组合:有8名男生和5名女生,从中任选6人有
- 有一个志愿者小组,共有6个人,其中男生3人
- ①判断下面各题的两种数量是否成比例?并说明


 (1)设y=a(x+1)(x-6)(a≠0),
(1)设y=a(x+1)(x-6)(a≠0),