思路解析：结合独立性检验的本质来解释比较合适.

可以有约95%以上的把握认为“性别与喜欢数学课之间有关系”.作出这样判断的依据是独立性检验的基本思想，具体过程如下:

分别用a、b、c、d表示样本中的喜欢数学课的男生人数、不喜欢数学课的男生人数、喜欢数学课的女生人数、不喜欢数学课的女生人数.

如果性别与是否喜欢数学课有关系，则男生中喜欢数学课的比例 与女生中喜欢数学课的比例 应该相差很多，即| - |=| |应很大.

将上式等号右边乘以常数因子 ，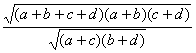

然后平方得K ² = (其中n=a+b+c+d为样本总量).

因此K ² 越大，“性别与喜欢数学课之间有关系”成立的可能性越大.

另一方面，假设“性别与喜欢数学课之间没有关系”，由于事件A=｛K ² ≥3.841｝的概率为P(K ² ≥3.841)≈0.05，因此事件A是一个小概率事件，而由样本数据计算得K ² ≈4.513，这表明小概率事件A发生.

    根据假设检验的基本原理，我们应该断定“性别与喜欢数学课之间有关系”成立，并且这种判断出错的可能性约为5%.所以约有95%的把握认为“性别与喜欢数学课之间有关系”.

思路解析：结合独立性检验的本质来解释比较合适.

可以有约95%以上的把握认为“性别与喜欢数学课之间有关系”.作出这样判断的依据是独立性检验的基本思想，具体过程如下:

分别用a、b、c、d表示样本中的喜欢数学课的男生人数、不喜欢数学课的男生人数、喜欢数学课的女生人数、不喜欢数学课的女生人数.

如果性别与是否喜欢数学课有关系，则男生中喜欢数学课的比例 与女生中喜欢数学课的比例 应该相差很多，即| - |=| |应很大.

将上式等号右边乘以常数因子 ，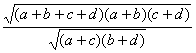

然后平方得K ² = (其中n=a+b+c+d为样本总量).

因此K ² 越大，“性别与喜欢数学课之间有关系”成立的可能性越大.

另一方面，假设“性别与喜欢数学课之间没有关系”，由于事件A=｛K ² ≥3.841｝的概率为P(K ² ≥3.841)≈0.05，因此事件A是一个小概率事件，而由样本数据计算得K ² ≈4.513，这表明小概率事件A发生.

    根据假设检验的基本原理，我们应该断定“性别与喜欢数学课之间有关系”成立，并且这种判断出错的可能性约为5%.所以约有95%的把握认为“性别与喜欢数学课之间有关系”.