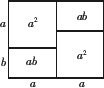
通过计算几何图形的面积可得到一些代数恒等式,如图,可以得到的代数恒等式是 [ ] A. (a-b)2=a2-2ab+b2 B. (a+b)2=a2+2ab+b2 C. 2a(a+b)=2a2+2ab D. (a+b)(a-b)=a2-b2
2019-05-07
| |||||||||||||||