阅读材料:例:说明代数式 x2+1 + (x-3)2+4 的几何意义,并求它的最小值.解: x2+1 + (x-3)2+4 =" (x-0)2+12" + (x-3)2+22 ,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则 (x-0)2+12 可以看成点P与点A(0,1)的距离, (x-3)2+22 可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.设点A关于x轴的对称点为A′,则PA=PA′,因此,求PA+PB的最小值,只需
2019-05-07
| 阅读材料: 例:说明代数式 x2+1 + (x-3)2+4 的几何意义,并求它的最小值. 解: x2+1 + (x-3)2+4 =" (x-0)2+12" + (x-3)2+22 ,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则 (x-0)2+12 可以看成点P与点A(0,1)的距离, (x-3)2+22 可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值. 设点A关于x轴的对称点为A′,则PA=PA′,因此,求PA+PB的最小值,只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,所以PA′+PB的最小值为线段A′B的长度.为此,构造直角三角形A′CB,因为A′C=3,CB=3,所以A′B="3" 2 ,即原式的最小值为3 2 . 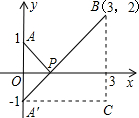 根据以上阅读材料,解答下列问题: (1)代数式 (x-1)2+1 + (x-2)2+9 的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B (2,3)的距离之和.(填写点B的坐标) (2)代数式 x2+49 + x2-12x+37 的最小值为. |
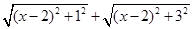 的形式,
的形式, 的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B(2,3)的距离之和,
的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B(2,3)的距离之和, 的形式,
的形式,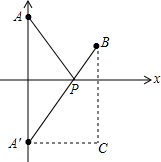
 ,
,