某校组织高一数学模块检测(满分150分),从得分在[90,140]的学生中随机抽取了100名学生的成绩,将它们分成5组,分别为:第1组[90,100),第2组[100,110),第3组[110,120),第4组[120,130),第5组[130,140],然后绘制成频率分布直方图.(I)求成绩在[120,130)内的频率,并将频率分布直方图补齐;(Ⅱ)从成绩在[110,120),[120,130),[130,140]这三组的学生中,用分层抽样的方法选取n名学生参加一项活动,已知从成绩在[120,130)内
2019-06-25
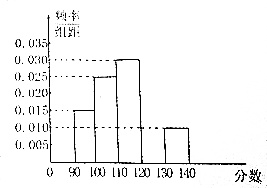
某校组织高一数学模块检测(满分150分),从得分在[90,140]的学生中随机抽取了100名学生的成绩,将它们分成5组,分别为:第1组[90,100),第2组[100,110),第3组[110,120),第4组[120,130),第5组[130,140],然后绘制成频率分布直方图.
(I)求成绩在[120,130)内的频率,并将频率分布直方图补齐;
(Ⅱ)从成绩在[110,120),[120,130),[130,140]这三组的学生中,用分层抽样的方法选取n名学生参加一项活动,已知从成绩在[120,130)内的学生中抽到了6人,求n的值;
(Ⅲ)从成绩在[120,130)内抽到的这6名学生中有4名男生,2名女生,现要从这6名学生中任选2名作为代表发言,求选取的2人恰为1男1女的概率.
优质解答
 (Ⅰ)由频率分布直方图在[120,130)内频率为:1-(0.015+0.025+0.30+0.010)×10=0.20;
(Ⅰ)由频率分布直方图在[120,130)内频率为:1-(0.015+0.025+0.30+0.010)×10=0.20;
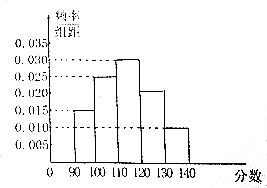
直方图如图所示:
(Ⅱ)[110,120)的人数为0.030×10×100=30人,
[120,130)的人数为0.020×100=20人
[130,140]人数为0.010×10×100=10人,
∴=.
∴n=18人
(Ⅲ)4名男生用A,B,C,D表示,2名女生用a,b表示,从这6名学生中任选2名作为代表发言则所有的基本事件有(A,B),(A,C),(A,D),(A,a),(A,b),(B,C),(B,D),(B,a),
(B,b),(C,D),(C,a),(C,b),(D,a),(D,b),(a,b),共15个,
其中取的2人恰为1男1女的有(A,a),(A,b),(B,a),(B,b),(C,a),(C,b),(D,a),(D,b)共8个,
故选取的2人恰为1男1女的概率为.
 (Ⅰ)由频率分布直方图在[120,130)内频率为:1-(0.015+0.025+0.30+0.010)×10=0.20;
(Ⅰ)由频率分布直方图在[120,130)内频率为:1-(0.015+0.025+0.30+0.010)×10=0.20;
直方图如图所示:
(Ⅱ)[110,120)的人数为0.030×10×100=30人,
[120,130)的人数为0.020×100=20人
[130,140]人数为0.010×10×100=10人,
∴=.
∴n=18人
(Ⅲ)4名男生用A,B,C,D表示,2名女生用a,b表示,从这6名学生中任选2名作为代表发言则所有的基本事件有(A,B),(A,C),(A,D),(A,a),(A,b),(B,C),(B,D),(B,a),
(B,b),(C,D),(C,a),(C,b),(D,a),(D,b),(a,b),共15个,
其中取的2人恰为1男1女的有(A,a),(A,b),(B,a),(B,b),(C,a),(C,b),(D,a),(D,b)共8个,
故选取的2人恰为1男1女的概率为.
相关问答
- 高中数学.设函数f(x)=x2+bx-al
- 高中数学,填空.在线等 1.已知正实数x,
- 在一条线段上任意取两点,将其分成三段,则这
- 高中平面基本性质的题目1.如果两个平面有两
- 高中函数问题函数图像既可以是连续的曲线,也
- 高中数学设函数f(x)=ax+lnX,g(
- 两道高中数学题向量OA,OB,OC为空间的
- 高二数学、过正方体的每三个顶点都可确定一个
- 请教一个高二数学立体几何关于异面直线的题目
- 高中数学求解在曲线y=x^2过哪一点的切线
- 怎样理解曲线上某点处的切线只有一条,而过某
- 两道关于平面向量的高中数学题1.知两单位向
- 高中数学参数方程与轨迹方程的问题直线C参数
- 高中数学必修2点到直线方程的距离,1.已知
- 高中数学关于一元二次函数抛物线等问题抛物线
- 例题:已知圆C:(x+1)^2+y^2=1


 (Ⅰ)由频率分布直方图在[120,130)内频率为:1-(0.015+0.025+0.30+0.010)×10=0.20;
(Ⅰ)由频率分布直方图在[120,130)内频率为:1-(0.015+0.025+0.30+0.010)×10=0.20;