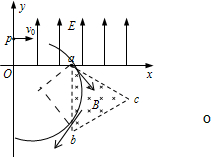
如图所示的平面直角坐标系xoy，在第Ⅰ象限内有平行于y轴的匀强电场，方向沿y正方向；在第Ⅳ象限的正三角形abc区域内有匀强电场，方向垂直于xoy平面向里，正三角形边长为L，且ab边与y轴平行．一质量为m、电荷量为q的粒子，从y轴上的P（0，h）点，以大小为v0的速度沿x轴正方向射入电场，通过电场后从x轴上的a（2h，0）点进入第Ⅳ象限，又经过磁场从y轴上的某点Q进入第Ⅲ象限，且速度与y轴负方向成45°角，不计粒子所受的重力．求：（1）电场强度E的大小；（2）粒子到达a点时速度的大小和方向；（3）abc区域
如图所示的平面直角坐标系xoy，在第Ⅰ象限内有平行于y轴的匀强电场，方向沿y正方向；在第Ⅳ象限的正三角形abc区域内有匀强电场，方向垂直于xoy平面向里，正三角形边长为L，且ab边与y轴平行．一质量为m、电荷量为q的粒子，从y轴上的P（0，h）点，以大小为v0的速度沿x轴正方向射入电场，通过电场后从x轴上的a（2h，0）点进入第Ⅳ象限，又经过磁场从y轴上的某点Q进入第Ⅲ象限，且速度与y轴负方向成45°角，不计粒子所受的重力．求：
（1）电场强度E的大小；
（2）粒子到达a点时速度的大小和方向；
（3）abc区域内磁场的磁感应强度B的最小值；
（4）在（3）情况下带电粒子从P点运动到Q点历经多长时间．
2019-06-26
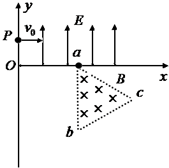
如图所示的平面直角坐标系xoy，在第Ⅰ象限内有平行于y轴的匀强电场，方向沿y正方向；在第Ⅳ象限的正三角形abc区域内有匀强电场，方向垂直于xoy平面向里，正三角形边长为L，且ab边与y轴平行．一质量为m、电荷量为q的粒子，从y轴上的P（0，h）点，以大小为v0的速度沿x轴正方向射入电场，通过电场后从x轴上的a（2h，0）点进入第Ⅳ象限，又经过磁场从y轴上的某点Q进入第Ⅲ象限，且速度与y轴负方向成45°角，不计粒子所受的重力．求：（1）电场强度E的大小；
（2）粒子到达a点时速度的大小和方向；
（3）abc区域内磁场的磁感应强度B的最小值；
（4）在（3）情况下带电粒子从P点运动到Q点历经多长时间．
