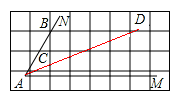
“三等分任意角”是数学史上一个著名问题 已知一个角∠MAN设 (Ⅰ)当∠MAN=69 0 时, 的大小为 ▲ (度);(Ⅱ)如图,将∠MAN放置在每个小正方形的边长为1cm的网格中,角的一边AM与水平方向的网格线平行,另一边AN经过格点B,且AB=2.5cm.现要求只能使用带刻度的直尺,请你在图中作出 ,并简要说明作法(不要求证明) ▲ .
2019-05-07
| “三等分任意角”是数学史上一个著名问题  已知一个角∠MAN设 已知一个角∠MAN设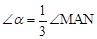 (Ⅰ)当∠MAN=69 0 时, 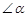 的大小为 ▲ (度); 的大小为 ▲ (度);(Ⅱ)如图,将∠MAN放置在每个小正方形的边长为1cm的网格中,角的一边AM与水平方向的网格线平行,另一边AN经过格点B,且AB=2.5cm.现要求只能使用带刻度的直尺,请你在图中作出 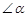 ,并简要说明作法(不要求证明) ▲ . ,并简要说明作法(不要求证明) ▲ .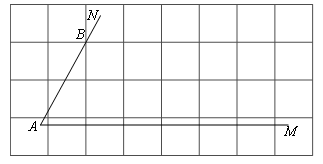 |
 ,计算即可得
,计算即可得