任给一些不同的实数 n ，得到不同的抛物线 ，如当 n=0 ，± 2 时，关于这些抛物线有以下结论：①开口方向都相同；②对称轴都相同；③形状都相同；④都有最低点，其中判断正确的个数是 ( ) A ． 1 个 B ． 2 个 C ． 3 个 D ． 4 个
2020-04-29
任给一些不同的实数 n ，得到不同的抛物线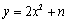 
，如当 n=0 ，± 2 时，关于这些抛物线有以下结论：①开口方向都相同；②对称轴都相同；③形状都相同；④都有最低点，其中判断正确的个数是 ( )
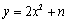，如当 n=0 ，± 2 时，关于这些抛物线有以下结论：①开口方向都相同；②对称轴都相同；③形状都相同；④都有最低点，其中判断正确的个数是 ( )
A ． 1 个 B ． 2 个 C ． 3 个 D ． 4 个