数学
如图，某数学兴趣小组在活动课上测量学校旗杆的高度．已知小亮站着测量，眼睛与地面的距离（AB）是1.7米，看旗杆顶部E的仰角为30°；小敏蹲着测量，眼睛与地面的距离（CD）是0.7米，看旗杆顶部E的仰角为45°．两人相距5米且位于旗杆同侧（点B、D、F在同一直线上）． （1）求小敏到旗杆的距离DF．（结果保留根号）（2）求旗杆EF的高度．（结果保留整数，参考数据：2≈1.4，3≈1.7）

2019-06-02

如图，某数学兴趣小组在活动课上测量学校旗杆的高度．已知小亮站着测量，眼睛与地面的距离（AB）是1.7米，看旗杆顶部E的仰角为30°；小敏蹲着测量，眼睛与地面的距离（CD）是0.7米，看旗杆顶部E的仰角为45°．两人相距5米且位于旗杆同侧（点B、D、F在同一直线上）．
作业帮
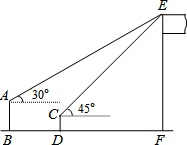
（1）求小敏到旗杆的距离DF．（结果保留根号）
（2）求旗杆EF的高度．（结果保留整数，参考数据：
2
≈1.4，
3
≈1.7）
优质解答
（1）过点A作AM⊥EF于点M，过点C作CN⊥EF于点N，
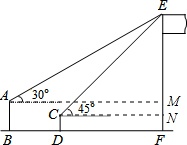作业帮设CN=x，
在Rt△ECN中，
∵∠ECN=45°，
∴EN=CN=x，
∴EM=x+0.7-1.7=x-1，
∵BD=5，
∴AM=BF=5+x，
在Rt△AEM中，
∵∠EAM=30°
∴
EM
AM
=
3
3
，
∴x-1=
3
3
（x+5），
解得：x=4+3
3
，
即DF=（4+3
3
）（米）；
（2）由（1）得：
EF=x+0.7=4+3
3
+0.7
≈4+3×1.7+0.7
≈9.8≈10（米）．
答：旗杆的高度约为10米． （1）过点A作AM⊥EF于点M，过点C作CN⊥EF于点N，
作业帮设CN=x，
在Rt△ECN中，
∵∠ECN=45°，
∴EN=CN=x，
∴EM=x+0.7-1.7=x-1，
∵BD=5，
∴AM=BF=5+x，
在Rt△AEM中，
∵∠EAM=30°
∴
EM
AM
=
3
3
，
∴x-1=
3
3
（x+5），
解得：x=4+3
3
，
即DF=（4+3
3
）（米）；
（2）由（1）得：
EF=x+0.7=4+3
3
+0.7
≈4+3×1.7+0.7
≈9.8≈10（米）．
答：旗杆的高度约为10米．
相关问答