如图,在△ABC中,∠ABC=90°,AB=3,BC=1,P为△ABC内一点,∠BPC=90° (Ⅰ)若PB=12,求PA;(Ⅱ)若∠APB=150°,求tan∠PBA.
2019-04-22
如图,在△ABC中,∠ABC=90°,AB=
,BC=1,P为△ABC内一点,∠BPC=90°
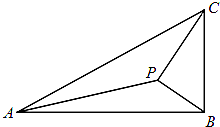
(Ⅰ)若PB=
,求PA;
(Ⅱ)若∠APB=150°,求tan∠PBA.
| 3 |

(Ⅰ)若PB=
| 1 |
| 2 |
(Ⅱ)若∠APB=150°,求tan∠PBA.