为了研究某学科成绩是否与学生性别有关,采用分层抽样的方法,从高三年级抽取了30名男生和20名女生的该学科成绩,得到如所示男生成绩的频率分布直方图和女生成绩的茎叶图,规定80分以上为优分(含80分).(Ⅰ)(i)请根据图示,将2×2列联表补充完整;优分非优分总计男生女生总计50(ii)据此列联表判断,能否在犯错误概率不超过10%的前提下认为“该学科成绩与性别有关”?(Ⅱ)将频率视作概率,从高三年级该学科成绩中任意抽取3名学生的成绩,求成绩为优分人数X的期望和方差.P(K2≥k)0.1000.0500.010
2019-05-04
为了研究某学科成绩是否与学生性别有关,采用分层抽样的方法,从高三年级抽取了30名男生和20名女生的该学科成绩,得到如所示男生成绩的频率分布直方图和女生成绩的茎叶图,规定80分以上为优分(含80分).
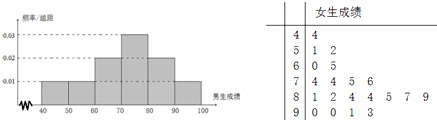
(Ⅰ)(i)请根据图示,将2×2列联表补充完整;
(ii)据此列联表判断,能否在犯错误概率不超过10%的前提下认为“该学科成绩与性别有关”?
(Ⅱ)将频率视作概率,从高三年级该学科成绩中任意抽取3名学生的成绩,求成绩为优分人数X的期望和方差.
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
附:K2=| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
.
优质解答
(Ⅰ)根据图示,将2×2列联表补充完整如下:
| 优分 | 非优分 | 总计 |
| 男生 | 9 | 21 | 30 |
| 女生 | 11 | 9 | 20 |
| 总计 | 20 | 30 | 50 |
假设H0:该学科成绩与性别无关,
则K2的观测值k=| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
=| 50×(9×9-11×21)2 |
| 20×30×20×30 |
=3.125,
因为3.125>2.706,
所以能在犯错误概率不超过10%的前提下认为该学科成绩与性别有关.
(Ⅱ)由于有较大的把握认为该学科成绩与性别有关,
因此需要将男女生成绩的优分频率f==0.4视作概率;
设从高三年级中任意抽取3名学生的该学科成绩中,优分人数为X,
则X服从二项分布B(3,0.4),
所求概率P=P(X=2)+P(X=3)
=×0.42×0.6+×0.43
=0.352.
(Ⅰ)根据图示,将2×2列联表补充完整如下:
| 优分 | 非优分 | 总计 |
| 男生 | 9 | 21 | 30 |
| 女生 | 11 | 9 | 20 |
| 总计 | 20 | 30 | 50 |
假设H0:该学科成绩与性别无关,
则K2的观测值k=| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
=| 50×(9×9-11×21)2 |
| 20×30×20×30 |
=3.125,
因为3.125>2.706,
所以能在犯错误概率不超过10%的前提下认为该学科成绩与性别有关.
(Ⅱ)由于有较大的把握认为该学科成绩与性别有关,
因此需要将男女生成绩的优分频率f==0.4视作概率;
设从高三年级中任意抽取3名学生的该学科成绩中,优分人数为X,
则X服从二项分布B(3,0.4),
所求概率P=P(X=2)+P(X=3)
=×0.42×0.6+×0.43
=0.352.

