数学
（2011•合肥二模）高三年级在综合素质评价的某个维度的测评中，依据评分细则，学生之间相互打分，最终将所有的数据合成一个分数，满分100分．按照大于等于80分为优秀，小于80分为合格．为了解学生在该维度的测评结果，从毕业班中随机抽出一个班的数据．该班共有60名学生，得到如下的列联表．（2）能否在犯错误的概率不超过0.10的前提下认为性别与测评结果有关系？（3）如果想了解全年级学生该维度的表现情况，采取简单随机抽样的方式在全校学生中抽取少数一部分人来分析，请你选择一个合适的抽样方法，并解释理由；（4）学生代

2019-06-13

（2011•合肥二模）高三年级在综合素质评价的某个维度的测评中，依据评分细则，学生之间相互打分，最终将所有的数据合成一个分数，满分100分．按照大于等于80分为优秀，小于80分为合格．为了解学生在该维度的测评结果，从毕业班中随机抽出一个班的数据．该班共有60名学生，得到如下的列联表．

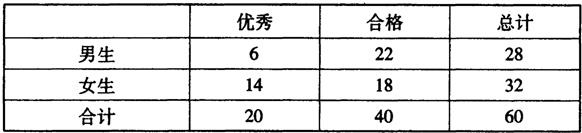
（2）能否在犯错误的概率不超过0.10的前提下认为性别与测评结果有关系？
（3）如果想了解全年级学生该维度的表现情况，采取简单随机抽样的方式在全校学生中抽取少数一部分人来分析，请你选择一个合适的抽样方法，并解释理由；
（4）学生代表、教师代表、家长代表、教务员四人，分别对测评结果是优秀的20名学生进行检查，检查他们是否躲优秀的相4名检查人员各自纖立的舰20学生中随机抽取一名，设其中男生的人数为随机变量x，求随机变量x的分布列期望．
优质解答
（1）提出统计假设：性别与测评结果没有关系，则
K2＝
60×(6×18−22×14)2
40×20×32×28
＝3.348＞2.706，
P（K2＞2.706）=0.10，
因此，在犯错误的概率不超过0.10的前提下认为“性别与测试结果有关系”．
（2）有（1）可知性别很有可能对是否优秀有影响，所以采用分层抽样按男女生比例抽取一定的学生，这样得到的结果对学生在该维度总体表现情况会比较符合实际情况；
（3）四名抽查人员，从20名学生中随即抽取一名是男生的概率是P=
3
10
，随机变量X的可能取值为：0，1，2，3，4．
∴P(X＝0)＝ 
C
0
4
(
3
10
)0(
7
10
)4＝(
7
10
)4，P(X＝1)＝
C
1
4
(
3
10
)1(
7
10
)3＝
12×73
104
，
P(X＝2)＝
C
2
4
(
3
10
)2(
7
10
)2＝
6×32×72
104
，
P（X=3）=
C
3
4
(
3
10
)3(
7
10
)1，
p（X=4）=
C
4
4
(
3
10
)4，
∴随机变量X的分布列为：
X 01 2 3 4
P (
7
10
)4
C
1
4
 (
3
10
)(
7
10
)3		K2＝
60×(6×18−22×14)2
40×20×32×28
＝3.348＞2.706，
P（K2＞2.706）=0.10，
因此，在犯错误的概率不超过0.10的前提下认为“性别与测试结果有关系”．
（2）有（1）可知性别很有可能对是否优秀有影响，所以采用分层抽样按男女生比例抽取一定的学生，这样得到的结果对学生在该维度总体表现情况会比较符合实际情况；
（3）四名抽查人员，从20名学生中随即抽取一名是男生的概率是P=
3
10
，随机变量X的可能取值为：0，1，2，3，4．
∴P(X＝0)＝ 
C
0
4
(
3
10
)0(
7
10
)4＝(
7
10
)4，P(X＝1)＝
C
1
4
(
3
10
)1(
7
10
)3＝
12×73
104
，
P(X＝2)＝
C
2
4
(
3
10
)2(
7
10
)2＝
6×32×72
104
，
P（X=3）=
C
3
4
(
3
10
)3(
7
10
)1，
p（X=4）=
C
4
4
(
3
10
)4，
∴随机变量X的分布列为：
X 01 2 3 4
P (
7
10
)4
C
1
4
 (
3
10
)(
7
10
)3
相关问答