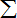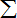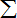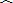数学
为了对某校高三（1）班9月调考成绩进行分析，在全班同学中随机抽出5位，他们的数学分数（已折算为百分制）从小到大排列为75、80、85、90、95，物理分数从小到大排列为 73、77、80、87、88．（I）求这5位同学中恰有2位同学的数学和物理分数都不小于85分的概率；（II）若这5位同学的数学、物理、化学分数事实上对应如下表：从散点图分析，y与x，z与x之间都有较好的线性相关关系，分别求y与x，z与x的线性回归方程，并用相关指数比较所求回归模型的拟合效果．参考数据：.x＝85，.y＝81，.z

2019-04-19

为了对某校高三（1）班9月调考成绩进行分析，在全班同学中随机抽出5位，他们的数学分数（已折算为百分制）从小到大排列为75、80、85、90、95，物理分数从小到大排列为 73、77、80、87、88．
（I）求这5位同学中恰有2位同学的数学和物理分数都不小于85分的概率；
（II）若这5位同学的数学、物理、化学分数事实上对应如下表：
从散点图分析，y与x，z与x之间都有较好的线性相关关系，分别求y与x，z与x的线性回归方程，并用相关指数比较所求回归模型的拟合效果．
参考数据：
.
x
＝85，
.
y
＝81，
.
z
＝86，
5
i＝1
(xi−
.
x
)2=250，
5
i＝1
(yi−
.
y
) 2＝166，
5
i＝1
(zi−
.
z
) 2＝100，
5
i＝1
 (xi−
.
x
)(yi−
.
y
)  ＝200，
5
i＝1
 (xi−
.
x
)(zi−
.
z
)  ＝150．
优质解答
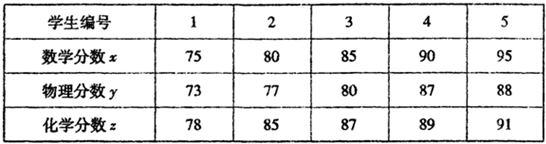
（I）这5位同学中恰有2位同学的数学和物理分数均为不小于85分，
则需要先从数学的3个不小于85分数中选出2个与2个物理不小于85分数对应，
种数是C32A22（或A32），然后将剩下的3个数学分数和物理分数任意对应，种数是A33．
据乘法原理，满足条件的种数是C32A22A33． （2分）
这5位同学的物理分数和数学分数分别对应的种数共有A55． （5分）
故所求的概率P＝
C
2
3
A
2
2
A
3
3
A
5
5
＝
3
10
． （4分）
（II）设y与x、z与x的线性回归方程分别是
̂
y
＝bx+a、
̂
z
＝b′x+a′．
根据所给的数据，可以计算出b＝
200
250
＝0.8，a＝81−0.8×85＝13，b′＝
150
250
＝0.6，a′＝86−0.6×85＝35．（8分）
所以y与x和z与x的回归方程分别是
̂
y
＝0.6x+13、
̂
z
＝0.6x+35．（11分）
∴
5
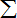i＝1
（yi-
y
i）2=02+02+（-1）2+22+（-1）2=6，
∴
5
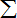i＝1
（zi-
z
i）2=（-2）2+22+12+02+（-1）2=10，
又y与x、z与x的相关指数是R2＝1−
6
166
≈0.964、R′2＝1−
10
100
≈0.90． （11分）
故回归模型
̂
y
＝0.6x+13比回归模型
̂
z
＝0.6x+35的拟合的效果好．（12分）] （I）这5位同学中恰有2位同学的数学和物理分数均为不小于85分，
则需要先从数学的3个不小于85分数中选出2个与2个物理不小于85分数对应，
种数是C32A22（或A32），然后将剩下的3个数学分数和物理分数任意对应，种数是A33．
据乘法原理，满足条件的种数是C32A22A33． （2分）
这5位同学的物理分数和数学分数分别对应的种数共有A55． （5分）
故所求的概率P＝
C
2
3
A
2
2
A
3
3
A
5
5
＝
3
10
． （4分）
（II）设y与x、z与x的线性回归方程分别是
̂
y
＝bx+a、
̂
z
＝b′x+a′．
根据所给的数据，可以计算出b＝
200
250
＝0.8，a＝81−0.8×85＝13，b′＝
150
250
＝0.6，a′＝86−0.6×85＝35．（8分）
所以y与x和z与x的回归方程分别是
̂
y
＝0.6x+13、
̂
z
＝0.6x+35．（11分）
∴
5
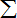i＝1
（yi-
y
i）2=02+02+（-1）2+22+（-1）2=6，
∴
5
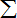i＝1
（zi-
z
i）2=（-2）2+22+12+02+（-1）2=10，
又y与x、z与x的相关指数是R2＝1−
6
166
≈0.964、R′2＝1−
10
100
≈0.90． （11分）
故回归模型
̂
y
＝0.6x+13比回归模型
̂
z
＝0.6x+35的拟合的效果好．（12分）]
相关问答