如图，点E是矩形ABCD中CD边上一点，△BCE沿BE折叠为△BFE，点F落在AD上． （1）求证：△ABF∽△DFE；（2）若△BEF也与△ABF相似，请求出BCCD的值．
2019-04-10
如图，点E是矩形ABCD中CD边上一点，△BCE沿BE折叠为△BFE，点F落在AD上．
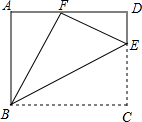
（1）求证：△ABF∽△DFE；
（2）若△BEF也与△ABF相似，请求出的值．
优质解答
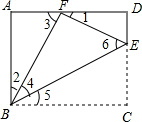（1）证明：在矩形ABCD中，∠A=∠C=∠D=90°，
又由折叠的性质知△BCE≌△BFE，
∴∠BFE=∠C=90°，
∵∠2+∠3=∠1+∠3=90°，
∴∠2=∠1，
∴△ABF∽△DFE；
（2）①当△ABF∽△FBE时，∠2=∠4．
∵∠4=∠5，∠2+∠4+∠5=90°，
∴∠2=∠4=∠5=30°，
∴设CE=EF=x，则BC=x，DE=x，
∴DC=x，
∴==；
②当△ABF∽△FEB时，∠2=∠6，
∵∠4+∠6=90°，
∴∠2+∠4=90°，
这与∠2+∠4+∠5=90°相矛盾，
∴△ABF∽△FEB不成立．
综上所述，的值是．
（1）证明：在矩形ABCD中，∠A=∠C=∠D=90°，
又由折叠的性质知△BCE≌△BFE，
∴∠BFE=∠C=90°，
∵∠2+∠3=∠1+∠3=90°，
∴∠2=∠1，
∴△ABF∽△DFE；
（2）①当△ABF∽△FBE时，∠2=∠4．
∵∠4=∠5，∠2+∠4+∠5=90°，
∴∠2=∠4=∠5=30°，
∴设CE=EF=x，则BC=x，DE=x，
∴DC=x，
∴==；
②当△ABF∽△FEB时，∠2=∠6，
∵∠4+∠6=90°，
∴∠2+∠4=90°，
这与∠2+∠4+∠5=90°相矛盾，
∴△ABF∽△FEB不成立．
综上所述，的值是．
相关问答
- 平面X平行平面Y,A和C属于平面X,B和D
- 如图9,直线y=-1/2x+b与两坐标轴相
- 在矩形ABCD中,E为AD中点,EF垂直于
- 在Rt三角形ABC中,角C=90度,以斜边
- O是△ABC内一点且∠AOB=∠AOC,∠
- 如图,△ABC的中线BE,CF相交于点G,
- 如图，四条线段的长分别为9，5，x、1（其
- 如图已知BF,CF分别是三角形ABC的边A
- 如果一个直角三角形的两条边长分别是6和8，
- 已知d e f分别在三角形abc的边ab,
- 在三角形abc中ac=25ab=35tan
- 如图，已知△ABC∽△DEF，求未知边x，
- 三角形ABC中,角A=60度,BE,CF分
- 如图,角BAE=90°,AB=AC=CD=
- 关于相似三角形的问题(急~)已知:如图,在
- 如图，在矩形ABCD中，DC=2，CF⊥B