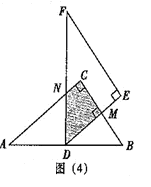
数学活动——求重叠部分的面积。问题情境:数学活动课上,老师出示了一个问题: 如图(1),将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合,DE经过点C,DF交AC于点G。求重叠部分(△DCG)的面积。(1)独立思考:请解答老师提出的问题。(2)合作交流:“希望”小组受此问题的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图(2),你能求出重叠部分(△DGH)的面积吗?请写出解答过程。(
2019-04-14
| 数学活动——求重叠部分的面积。 问题情境:数学活动课上,老师出示了一个问题: 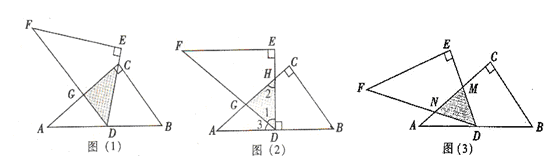 如图(1),将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合,DE经过点C,DF交AC于点G。 求重叠部分(△DCG)的面积。 (1)独立思考:请解答老师提出的问题。 (2)合作交流:“希望”小组受此问题的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图(2),你能求出重叠部分(△DGH)的面积吗?请写出解答过程。 (3)提出问题:老师要求各小组向“希望”小组学习,将△DEF绕点D旋转,再提出一个求重叠部分面积的问题。“爱心”小组提出的问题是:如图(3),将△DEF绕点D旋转,DE,DF分别交AC于点M,N,使DM=MN,求重叠部分(△DMN)的面积。 任务:①请解决“爱心”小组所提出的问题,直接写出△DMN的面积是 . ②请你仿照以上两个小组,大胆提出一个符合老师要求的问题,并在图中画出图形,标明字母,不必解答(注:也可在图(1)的基础上按顺时针方向旋转)。 |
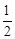 AC=
AC=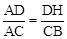 ,即
,即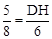 ,解得
,解得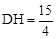 。
。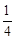 ×
×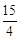 ×5=
×5=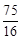 。
。