(1)先化简,再求值:(+1)÷,其中a=2+.(2)阅读下边一元二次方程求根公式的两种推导方法:方法一:(教材中方法)方法二:∵ax2+bx+c=0,∵ax2+bx+c=0,配方可得:∴4a2x2+4abx+4ac=0,a(x+)2=∴(2ax+b)2=b2-4ac.∴(x+)2=当b2-4ac≥0时,2ax+b=±,x+=±∴2ax=-b±.∴x=∴x=.请回答下列问题:(1)两种方法有什么异同?你认为哪个方法好?(2)说说你有什么感想?
2019-05-27
(1)先化简,再求值:(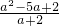 +1)÷
+1)÷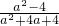 ,其中a=2+
,其中a=2+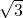 .
.
(2)阅读下边一元二次方程求根公式的两种推导方法:
方法一:(教材中方法)
方法二:
∵ax2+bx+c=0,∵ax2+bx+c=0,
配方可得:∴4a2x2+4abx+4ac=0,
a(x+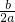 )2=
)2=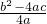 ∴(2ax+b)2=b2-4ac.
∴(2ax+b)2=b2-4ac.
∴(x+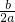 )2=
)2=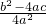
当b2-4ac≥0时,2ax+b=± ,
,
x+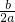 =±
=±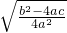 ∴2ax=-b±
∴2ax=-b± .
.
∴x=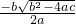 ∴x=
∴x=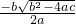 .
.
请回答下列问题:
(1)两种方法有什么异同?你认为哪个方法好?
(2)说说你有什么感想?
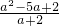 +1)÷
+1)÷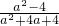 ,其中a=2+
,其中a=2+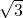 .
.(2)阅读下边一元二次方程求根公式的两种推导方法:
方法一:(教材中方法)
方法二:
∵ax2+bx+c=0,∵ax2+bx+c=0,
配方可得:∴4a2x2+4abx+4ac=0,
a(x+
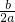 )2=
)2=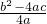 ∴(2ax+b)2=b2-4ac.
∴(2ax+b)2=b2-4ac.∴(x+
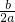 )2=
)2=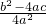
当b2-4ac≥0时,2ax+b=±
 ,
,x+
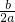 =±
=±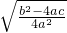 ∴2ax=-b±
∴2ax=-b± .
.∴x=
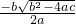 ∴x=
∴x=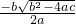 .
.请回答下列问题:
(1)两种方法有什么异同?你认为哪个方法好?
(2)说说你有什么感想?
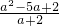 +1)÷
+1)÷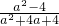
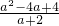 •
•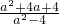 =
=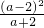 •
•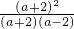 =a-2;
=a-2;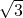 时,原式=2+
时,原式=2+