精选问答
如图1，E，F是正方形ABCD的边上两个动点，满足AE=DF，连接CF交BD于G，连接BE交AG于点H（1）求证：AG⊥BE；（2）如图2，连DH，若正方形的边长为4，则线段DH长度的最小值是25-225-2．

2019-05-03

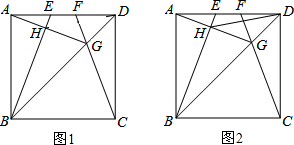
如图1，E，F是正方形ABCD的边上两个动点，满足AE=DF，连接CF交BD于G，连接BE交AG于点H
（1）求证：AG⊥BE；
（2）如图2，连DH，若正方形的边长为4，则线段DH长度的最小值是
2
5
-2
2
5
-2
．
优质解答
（1）证明：∵四边形ABCD是正方形，
∴AB=CD，∠BAD=∠ADC=90°，∠ADB=∠CDB=45°，
在△ABE和△DCF中，
AB＝CD
∠BAD＝∠ADC
AE＝DF
，
∴△ABE≌△DCF（SAS），
∴∠ABE=∠DCF，
在△ADG和△CDG中，
AD＝CD
∠ADB＝∠CDB
DG＝DG
，
∴△ADG≌△CDG（SAS），
∴∠DAG=∠DCF，
∴∠ABE=∠DAG，
∵∠DAG+∠BAH=90°，
∴∠BAE+∠BAH=90°，
∴∠AHB=90°，
∴AG⊥BE；

（2）取AB的中点O，连接OD、OH，
∵正方形的边长为4，
∴AO=OH=
1
2
×4=2，
由勾股定理得，OD=
42+22
=2
5
，
由三角形的三边关系得，O、D、H三点共线时，DH最小，
DH最小=2
5
-2．
故答案为：2
AB＝CD
∠BAD＝∠ADC
AE＝DF
，
∴△ABE≌△DCF（SAS），
∴∠ABE=∠DCF，
在△ADG和△CDG中，
AD＝CD
∠ADB＝∠CDB
DG＝DG
，
∴△ADG≌△CDG（SAS），
∴∠DAG=∠DCF，
∴∠ABE=∠DAG，
∵∠DAG+∠BAH=90°，
∴∠BAE+∠BAH=90°，
∴∠AHB=90°，
∴AG⊥BE；

（2）取AB的中点O，连接OD、OH，
∵正方形的边长为4，
∴AO=OH=
1
2
×4=2，
由勾股定理得，OD=
42+22
=2
5
，
由三角形的三边关系得，O、D、H三点共线时，DH最小，
DH最小=2
5
-2．
故答案为：2
相关问答