在某次数学考试中,考生的成绩 服从一个正态分布,即 ~N(90,100).(1)试求考试成绩 位于区间(70,110)上的概率是多少?(2)若这次考试共有2 000名考生,试估计考试成绩在(80,100)间的考生大约有多少人?
2019-05-30
| 在某次数学考试中,考生的成绩 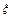 服从一个正态分布,即 服从一个正态分布,即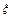 ~N(90,100). ~N(90,100).(1)试求考试成绩 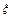 位于区间(70,110)上的概率是多少? 位于区间(70,110)上的概率是多少?(2)若这次考试共有2 000名考生,试估计考试成绩在(80,100)间的考生大约有多少人? |
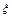 ~N(90,100),∴
~N(90,100),∴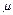 =90,
=90,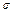 =
=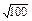 ="10. " 1分
="10. " 1分