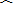下图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥.该圆锥的侧面展开图形是扇形OAB.经测量,纸杯上开口圆的直径为6cm,下底面直径为4cm,母线长EF=8cm.求扇形OAB的圆心角及这个纸杯的表面积.(面积计算结果用π表示).
2019-04-22
下图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥.该圆锥的侧面展开图形是扇形OAB.经测量,纸杯上开口圆的直径为6cm,下底面直径为4cm,母线长EF=8cm.求扇形OAB的圆心角及这个纸杯的表面积.(面积计算结果用π表示).
优质解答
由题意可知:=6π,=4π,设∠AOB=n,AO=R,则CO=R-8,
由弧长公式得:=6π,=4π,
∴,
解得:n=45,R=24,
故扇形OAB的圆心角是45度.
∵R=24,R-8=16,
∴S扇形OCD=×4π×16=32π(cm2),
S扇形OAB=×6π×24=72π(cm2),
纸杯侧面积=S扇形OAB-S扇形OCD=72π-32π=40π(cm2),
纸杯底面积=π•22=4π(cm2)
纸杯表面积=40π+4π=44π(cm2).
由题意可知:=6π,=4π,设∠AOB=n,AO=R,则CO=R-8,
由弧长公式得:=6π,=4π,
∴,
解得:n=45,R=24,
故扇形OAB的圆心角是45度.
∵R=24,R-8=16,
∴S扇形OCD=×4π×16=32π(cm2),
S扇形OAB=×6π×24=72π(cm2),
纸杯侧面积=S扇形OAB-S扇形OCD=72π-32π=40π(cm2),
纸杯底面积=π•22=4π(cm2)
纸杯表面积=40π+4π=44π(cm2).