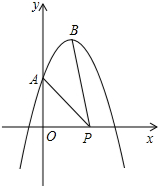
如图,抛物线y=-49x2+83x+2与y轴交于点A,顶点为B,点P是x轴上的一个动点,求线段PA与PB中较长的线段减去较短的线段的差的最小值与最大值,并求出相应的点P的坐标.
 如图,抛物线y=-
如图,抛物线y=-
x2+
x+2与y轴交于点A,顶点为B,点P是x轴上的一个动点,求线段PA与PB中较长的线段减去较短的线段的差的最小值与最大值,并求出相应的点P的坐标.
2019-05-03
 如图,抛物线y=-
如图,抛物线y=-| 4 |
| 9 |
| 8 |
| 3 |