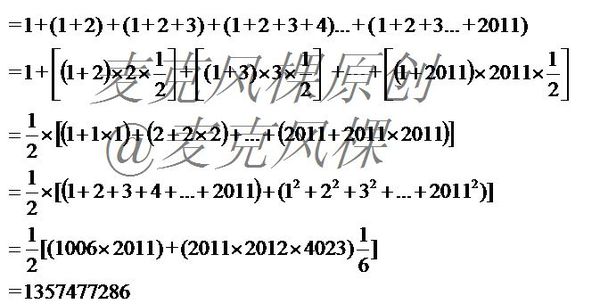原题= (1)+(1+2) + (1+2+3) + (1+2+3+4)...+ ( 1+2+3...+2011) 

= 1 + 3*2*½ +[ (1+3)*3*½] + ... + [(1+2011)*2011*½]  （高斯求和定理）

= ½*[(1+1*1）+（2+2*2）+（3+3*3）+……+(2011+2011*2011)]

= ½*[(1+2+3+4+5+6+7+8+9+10+11+12...+2011)+(1²+2²+3²+4²+...+2011²)]

带入1+2²+3²+...+n²=n(n+1)(2n+1)/6

= ½[(1006*2011)+(2011*2012*4023)/6]

=½(2023066+2712931506)

=1357477286

标准格式如下：

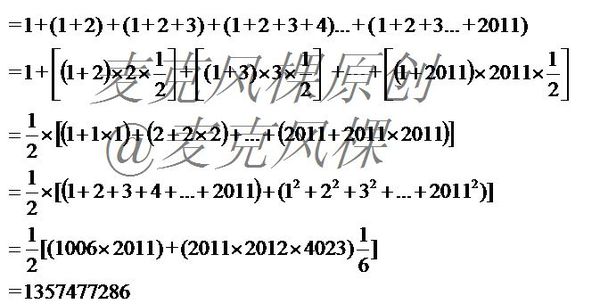
原题= (1)+(1+2) + (1+2+3) + (1+2+3+4)...+ ( 1+2+3...+2011) 

= 1 + 3*2*½ +[ (1+3)*3*½] + ... + [(1+2011)*2011*½]  （高斯求和定理）

= ½*[(1+1*1）+（2+2*2）+（3+3*3）+……+(2011+2011*2011)]

= ½*[(1+2+3+4+5+6+7+8+9+10+11+12...+2011)+(1²+2²+3²+4²+...+2011²)]

带入1+2²+3²+...+n²=n(n+1)(2n+1)/6

= ½[(1006*2011)+(2011*2012*4023)/6]

=½(2023066+2712931506)

=1357477286

标准格式如下：