精选问答
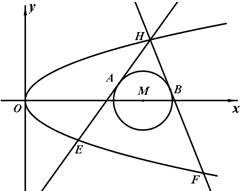
（2014•淄博三模）如图，已知抛物线C：y2=2px和⊙M：（x-4）2+y2=1，过抛物线C上一点H（x0，y0）（y0≥1）作两条直线与⊙M相切于A、两点，分别交抛物线为E、F两点，圆心点M到抛物线准线的距离为174．（Ⅰ）求抛物线C的方程；（Ⅱ）当∠AHB的角平分线垂直x轴时，求直线EF的斜率；（Ⅲ）若直线AB在y轴上的截距为t，求t的最小值．

2019-04-29

（2014•淄博三模）如图，已知抛物线C：y2=2px和⊙M：（x-4）2+y2=1，过抛物线C上一点H（x0，y0）（y0≥1）作两条直线与⊙M相切于A、两点，分别交抛物线为E、F两点，圆心点M到抛物线准线的距离为
17
4
．
（Ⅰ）求抛物线C的方程；
（Ⅱ）当∠AHB的角平分线垂直x轴时，求直线EF的斜率；
（Ⅲ）若直线AB在y轴上的截距为t，求t的最小值．
优质解答
（Ⅰ）∵点M到抛物线准线的距离为4+
p
2
=
17
4
，
∴p＝
1
2
，∴抛物线C的方程为y2=x．（2分）
（Ⅱ）法一：∵当∠AHB的角平分线垂直x轴时，点H（4，2），∴kHE=-kHF，
设E（x1，y1），F（x2，y2），∴
yH−y1
xH−x1
＝−
yH−y2
xH−x2
，∴
yH−y1
y
2
H
−
y
2
1
＝−
yH−y2
y
2
H
−
y
2
2
，
∴y1+y2=-2yH=-4．（5分）
∴kEF＝
y2−y1
x2−x1
＝
y2−y1
y
2
2
−
y
2
1
＝
1
y2+y1
＝−
1
4
．（7分）
法二：∵当∠AHB的角平分线垂直x轴时，点H（4，2），∴∠AHB=60°，可得kHA＝
3
，kHB＝−
4+
p
2
=
17
4
，
∴p＝
1
2
，∴抛物线C的方程为y2=x．（2分）
（Ⅱ）法一：∵当∠AHB的角平分线垂直x轴时，点H（4，2），∴kHE=-kHF，
设E（x1，y1），F（x2，y2），∴
yH−y1
xH−x1
＝−
yH−y2
xH−x2
，∴
yH−y1
y
2
H
−
y
2
1
＝−
yH−y2
y
2
H
−
y
2
2
，
∴y1+y2=-2yH=-4．（5分）
∴kEF＝
y2−y1
x2−x1
＝
y2−y1
y
2
2
−
y
2
1
＝
1
y2+y1
＝−
1
4
．（7分）
法二：∵当∠AHB的角平分线垂直x轴时，点H（4，2），∴∠AHB=60°，可得kHA＝
3
，kHB＝−
相关问答