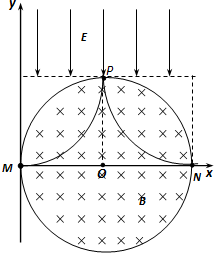
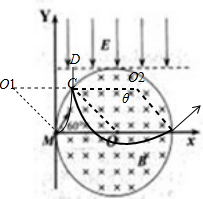
如图所示,真空中有一以O点为圆心的圆形匀强磁场区域,半径为R,磁场垂直纸面向里,在y>R的区域存在沿-y方向的云强电场,电场强度为E,在M点有一粒子源,辐射的粒子以相同的速率v沿不同方向射入第一象限,发现沿+x方向射入磁场的粒子穿出磁场进入电场,速度减小到0后又返回磁场,已知粒子的质量为m,电荷量为+q,粒子重力不计.(1)求圆形磁场区域磁感应强度的大小;(2)求沿+x方向射入磁场的粒子,从进入磁场到再次穿出磁场所走过的路程;(3)沿与+x方向成60°角射入的粒子,最终将从磁场边缘的N点(图中未画出)穿出
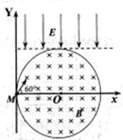 如图所示,真空中有一以O点为圆心的圆形匀强磁场区域,半径为R,磁场垂直纸面向里,在y>R的区域存在沿-y方向的云强电场,电场强度为E,在M点有一粒子源,辐射的粒子以相同的速率v沿不同方向射入第一象限,发现沿+x方向射入磁场的粒子穿出磁场进入电场,速度减小到0后又返回磁场,已知粒子的质量为m,电荷量为+q,粒子重力不计.
如图所示,真空中有一以O点为圆心的圆形匀强磁场区域,半径为R,磁场垂直纸面向里,在y>R的区域存在沿-y方向的云强电场,电场强度为E,在M点有一粒子源,辐射的粒子以相同的速率v沿不同方向射入第一象限,发现沿+x方向射入磁场的粒子穿出磁场进入电场,速度减小到0后又返回磁场,已知粒子的质量为m,电荷量为+q,粒子重力不计.
(1)求圆形磁场区域磁感应强度的大小;
(2)求沿+x方向射入磁场的粒子,从进入磁场到再次穿出磁场所走过的路程;
(3)沿与+x方向成60°角射入的粒子,最终将从磁场边缘的N点(图中未画出)穿出,不再进入磁场,求N点的坐标和粒子从M点运动到N点的总时间.
2019-06-26
 如图所示,真空中有一以O点为圆心的圆形匀强磁场区域,半径为R,磁场垂直纸面向里,在y>R的区域存在沿-y方向的云强电场,电场强度为E,在M点有一粒子源,辐射的粒子以相同的速率v沿不同方向射入第一象限,发现沿+x方向射入磁场的粒子穿出磁场进入电场,速度减小到0后又返回磁场,已知粒子的质量为m,电荷量为+q,粒子重力不计.
如图所示,真空中有一以O点为圆心的圆形匀强磁场区域,半径为R,磁场垂直纸面向里,在y>R的区域存在沿-y方向的云强电场,电场强度为E,在M点有一粒子源,辐射的粒子以相同的速率v沿不同方向射入第一象限,发现沿+x方向射入磁场的粒子穿出磁场进入电场,速度减小到0后又返回磁场,已知粒子的质量为m,电荷量为+q,粒子重力不计.(1)求圆形磁场区域磁感应强度的大小;
(2)求沿+x方向射入磁场的粒子,从进入磁场到再次穿出磁场所走过的路程;
(3)沿与+x方向成60°角射入的粒子,最终将从磁场边缘的N点(图中未画出)穿出,不再进入磁场,求N点的坐标和粒子从M点运动到N点的总时间.