优质解答
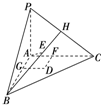证明：（1）如图所示，在平面ABC内取一点D，作DF⊥AC于F．
∵平面PAC⊥平面ABC，且交线为AC，∴DF⊥平面PAC．
又PA⊂平面PAC，∴DF⊥PA．
作DG⊥AB于G，同理可证：DG⊥PA．
∵DG、DF都在平面ABC内且DG∩DF=D，
∴PA⊥平面ABC；
（2）连结BE并延长交PC于H，
∵E是△PBC的垂心，∴PC⊥BH．
又已知AE是平面PBC的垂线，PC⊂平面PBC，
∴PC⊥AE．
又BH∩AE=E，∴PC⊥平面ABE．
又AB⊂平面ABE，∴PC⊥AB．
∵PA⊥平面ABC，∴PA⊥AB．
又PC∩PA=P，∴AB⊥平面PAC，
又AC⊂平面PAC，∴AB⊥AC，
即△ABC是直角三角形．证明：（1）如图所示，在平面ABC内取一点D，作DF⊥AC于F．
∵平面PAC⊥平面ABC，且交线为AC，∴DF⊥平面PAC．
又PA⊂平面PAC，∴DF⊥PA．
作DG⊥AB于G，同理可证：DG⊥PA．
∵DG、DF都在平面ABC内且DG∩DF=D，
∴PA⊥平面ABC；
（2）连结BE并延长交PC于H，
∵E是△PBC的垂心，∴PC⊥BH．
又已知AE是平面PBC的垂线，PC⊂平面PBC，
∴PC⊥AE．
又BH∩AE=E，∴PC⊥平面ABE．
又AB⊂平面ABE，∴PC⊥AB．
∵PA⊥平面ABC，∴PA⊥AB．
又PC∩PA=P，∴AB⊥平面PAC，
又AC⊂平面PAC，∴AB⊥AC，
即△ABC是直角三角形．
证明：（1）如图所示，在平面ABC内取一点D，作DF⊥AC于F．∵平面PAC⊥平面ABC，且交线为AC，∴DF⊥平面PAC．
又PA⊂平面PAC，∴DF⊥PA．
作DG⊥AB于G，同理可证：DG⊥PA．
∵DG、DF都在平面ABC内且DG∩DF=D，
∴PA⊥平面ABC；
（2）连结BE并延长交PC于H，
∵E是△PBC的垂心，∴PC⊥BH．
又已知AE是平面PBC的垂线，PC⊂平面PBC，
∴PC⊥AE．
又BH∩AE=E，∴PC⊥平面ABE．
又AB⊂平面ABE，∴PC⊥AB．
∵PA⊥平面ABC，∴PA⊥AB．
又PC∩PA=P，∴AB⊥平面PAC，
又AC⊂平面PAC，∴AB⊥AC，
即△ABC是直角三角形．
证明：（1）如图所示，在平面ABC内取一点D，作DF⊥AC于F．∵平面PAC⊥平面ABC，且交线为AC，∴DF⊥平面PAC．
又PA⊂平面PAC，∴DF⊥PA．
作DG⊥AB于G，同理可证：DG⊥PA．
∵DG、DF都在平面ABC内且DG∩DF=D，
∴PA⊥平面ABC；
（2）连结BE并延长交PC于H，
∵E是△PBC的垂心，∴PC⊥BH．
又已知AE是平面PBC的垂线，PC⊂平面PBC，
∴PC⊥AE．
又BH∩AE=E，∴PC⊥平面ABE．
又AB⊂平面ABE，∴PC⊥AB．
∵PA⊥平面ABC，∴PA⊥AB．
又PC∩PA=P，∴AB⊥平面PAC，
又AC⊂平面PAC，∴AB⊥AC，
即△ABC是直角三角形．