代数式的运算可以转化为五个多项式相乘,按多项式乘法法则,展开合并同类项后其乘积为:a5x5+a4x4+a3x3+a2x2+a1x+a,其中a5、a4、a3、a2、a1、a为乘积展开式各项的系数,因此,=a5x5+a4x4+a3x3+a2x2+a1x+a.(1)求a与a5的值;(2)求(a+a2+a4)2-(a1+a3+a5)2的值.
2019-05-07
代数式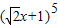 的运算可以转化为五个多项式
的运算可以转化为五个多项式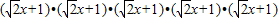 相乘,按多项式乘法法则,展开合并同类项后其乘积为:a5x5+a4x4+a3x3+a2x2+a1x+a,其中a5、a4、a3、a2、a1、a为乘积展开式各项的系数,因此,
相乘,按多项式乘法法则,展开合并同类项后其乘积为:a5x5+a4x4+a3x3+a2x2+a1x+a,其中a5、a4、a3、a2、a1、a为乘积展开式各项的系数,因此,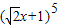 =a5x5+a4x4+a3x3+a2x2+a1x+a.
=a5x5+a4x4+a3x3+a2x2+a1x+a.
(1)求a与a5的值;
(2)求(a+a2+a4)2-(a1+a3+a5)2的值.
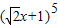 的运算可以转化为五个多项式
的运算可以转化为五个多项式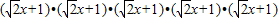 相乘,按多项式乘法法则,展开合并同类项后其乘积为:a5x5+a4x4+a3x3+a2x2+a1x+a,其中a5、a4、a3、a2、a1、a为乘积展开式各项的系数,因此,
相乘,按多项式乘法法则,展开合并同类项后其乘积为:a5x5+a4x4+a3x3+a2x2+a1x+a,其中a5、a4、a3、a2、a1、a为乘积展开式各项的系数,因此,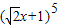 =a5x5+a4x4+a3x3+a2x2+a1x+a.
=a5x5+a4x4+a3x3+a2x2+a1x+a.(1)求a与a5的值;
(2)求(a+a2+a4)2-(a1+a3+a5)2的值.
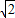 +1)5=a5+a4+a3+a2+a1+a①
+1)5=a5+a4+a3+a2+a1+a①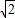 +1)5=-a5+a4-a3+a2-a1+a②
+1)5=-a5+a4-a3+a2-a1+a②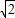 x+1)5=a5x5+a4x4+a3x3+a2x2+a1x+a,
x+1)5=a5x5+a4x4+a3x3+a2x2+a1x+a,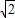 )5=4
)5=4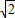 .
.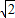 x+1)5=a5x5+a4x4+a3x3+a2x2+a1x+a在上述等式中:
x+1)5=a5x5+a4x4+a3x3+a2x2+a1x+a在上述等式中: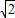 +1)5=a5+a4+a3+a2+a1+a,
+1)5=a5+a4+a3+a2+a1+a,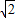 +1)5=-a5+a4-a3+a2-a1+a,
+1)5=-a5+a4-a3+a2-a1+a,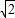 +1)5(-
+1)5(-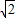 +1)5,
+1)5,