已知数列{a n }的前n项和为S n , ,满足S n 2 +2S n +1=a n S n (n ≥2).(I)计算S 1 ,S 2 ,S 3 ,S 4 ,猜想S n 的表达式;(II)并用数学归纳法证明.
2019-04-14
已知数列{a n }的前n项和为S n ,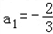 ,满足S n 2 +2S n +1=a n S n (n ≥2). ,满足S n 2 +2S n +1=a n S n (n ≥2).(I)计算S 1 ,S 2 ,S 3 ,S 4 ,猜想S n 的表达式; (II)并用数学归纳法证明. |
 ,
,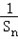 =a n ﹣2(n ≥2,n∈N),
=a n ﹣2(n ≥2,n∈N),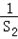 =a 2 ﹣2=S 2 ﹣a 1 ﹣2,
=a 2 ﹣2=S 2 ﹣a 1 ﹣2,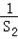 =
= ﹣2, ∴S 2 =﹣
﹣2, ∴S 2 =﹣ .
. ,S 4 =﹣
,S 4 =﹣ .
.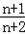 ,n∈N+,下边用数学归纳法证明:
,n∈N+,下边用数学归纳法证明: ,猜想成立.
,猜想成立.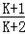 ,则
,则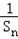 =a n ﹣2,∴
=a n ﹣2,∴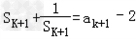 ,
, ,∴
,∴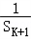 =
=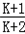 ﹣2=
﹣2=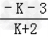 ,
,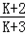 ,
,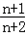 ,n∈N+成立.
,n∈N+成立.