如图，在平面直角坐标系xOy中，A（2，0），B（0，2），⊙C的圆心为点C（-1，0），半径为1．若D是⊙C上的一个动点，线段DA与y轴交于E点，则△ABE面积的最小值是（　　）A．2B．83C．2+22D．2−22

2019-05-03

下载本文

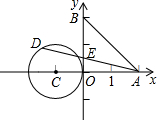如图，在平面直角坐标系xOy中，A（2，0），B（0，2），⊙C的圆心为点C（-1，0），半径为1．若D是⊙C上的一个动点，线段DA与y轴交于E点，则△ABE面积的最小值是（　　）

A．2
B．

8

3

C．2+

2

D．2−

2

优质解答

若△ABE的面积最小，则AD与⊙C相切，连接CD，则CD⊥AD；
Rt△ACD中，CD=1，AC=OC+OA=3；
由勾股定理，得：AD=2

2

；

∴S_△ACD=

1

2

AD•CD=

2

；
易证得△AOE∽△ADC，
∴

S△AOE

S△ADC

=（

OA

AD

）²=（

2

）²=

1

2

，
即S_△AOE=

1

2

S_△ADC=

2

；
∴S_△ABE=S_△AOB-S_△AOE=

1

2

×2×2-

2

=2-

2

；
故选D．若△ABE的面积最小，则AD与⊙C相切，连接CD，则CD⊥AD；
Rt△ACD中，CD=1，AC=OC+OA=3；
由勾股定理，得：AD=2

2

；