已知A,B,C是双曲线 x2 a2 - x2 b2 =1(a>0,b>0)上的三个点,AB过原点,AC经过右焦点F,若BF⊥AC且|BF|=|CF|,则该双曲线的渐近线方程为.
2019-12-16
已知A,B,C是双曲线 - =1(a>0,b>0)上的三个点,AB过原点,AC经过右焦点F,若BF⊥AC且
|BF|=|CF|,则该双曲线的渐近线方程为___.
优质解答
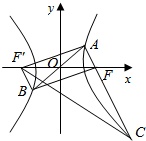 设左焦点为F′,连接AF′,BF′,CF′,
设左焦点为F′,连接AF′,BF′,CF′,
由OA=OB,OF=OF′,BF⊥AC,
可得四边形AFBF′为矩形,
设AF=m,则FC=FB=AF′=m+2a,CF′=m+4a,在直角△ACF′中,
(m+2a)2+(2a+2m)2=(m+4a)2,解得m=a,在直角△FAF′中,
AF2+AF′2=FF′2,即a2+(3a)2=(2c)2,
即4c2=10a2,即c=a,
b==a.
即有双曲线的渐近线方程为y=±x.
故答案为:y=±x.
 设左焦点为F′,连接AF′,BF′,CF′,
设左焦点为F′,连接AF′,BF′,CF′,
由OA=OB,OF=OF′,BF⊥AC,
可得四边形AFBF′为矩形,
设AF=m,则FC=FB=AF′=m+2a,CF′=m+4a,在直角△ACF′中,
(m+2a)2+(2a+2m)2=(m+4a)2,解得m=a,在直角△FAF′中,
AF2+AF′2=FF′2,即a2+(3a)2=(2c)2,
即4c2=10a2,即c=a,
b==a.
即有双曲线的渐近线方程为y=±x.
故答案为:y=±x.
 设左焦点为F′,连接AF′,BF′,CF′,
设左焦点为F′,连接AF′,BF′,CF′, 设左焦点为F′,连接AF′,BF′,CF′,
设左焦点为F′,连接AF′,BF′,CF′, 设左焦点为F′,连接AF′,BF′,CF′,
设左焦点为F′,连接AF′,BF′,CF′, 设左焦点为F′,连接AF′,BF′,CF′,
设左焦点为F′,连接AF′,BF′,CF′,