优质解答
 ∵直线ax+by=1与线段AB有一个公共点,
∵直线ax+by=1与线段AB有一个公共点,
∴点A(1,2),B(2,1)在直线ax+by=1的两侧(或过A,或过B),
∴(a+2b-1)(2a+b-1)≤0,
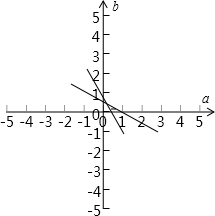
画出它们表示的平面区域,如图所示.
a2+b2表示原点到区域内的点的距离的平方,
由图可知,当原点O到直线2a+b-1=0的距离为原点到区域内的点的距离的最小值,即
∴a2+b2的最小值为
故选C. ∵直线ax+by=1与线段AB有一个公共点,
∵直线ax+by=1与线段AB有一个公共点,
∴点A(1,2),B(2,1)在直线ax+by=1的两侧(或过A,或过B),
∴(a+2b-1)(2a+b-1)≤0,
画出它们表示的平面区域,如图所示.
a2+b2表示原点到区域内的点的距离的平方,
由图可知,当原点O到直线2a+b-1=0的距离为原点到区域内的点的距离的最小值,即
∴a2+b2的最小值为
故选C.
 ∵直线ax+by=1与线段AB有一个公共点,
∵直线ax+by=1与线段AB有一个公共点,∴点A(1,2),B(2,1)在直线ax+by=1的两侧(或过A,或过B),
∴(a+2b-1)(2a+b-1)≤0,
画出它们表示的平面区域,如图所示.
a2+b2表示原点到区域内的点的距离的平方,
由图可知,当原点O到直线2a+b-1=0的距离为原点到区域内的点的距离的最小值,即
| 1 | ||
|
∴a2+b2的最小值为
| 1 |
| 5 |
故选C.
 ∵直线ax+by=1与线段AB有一个公共点,
∵直线ax+by=1与线段AB有一个公共点,∴点A(1,2),B(2,1)在直线ax+by=1的两侧(或过A,或过B),
∴(a+2b-1)(2a+b-1)≤0,
画出它们表示的平面区域,如图所示.
a2+b2表示原点到区域内的点的距离的平方,
由图可知,当原点O到直线2a+b-1=0的距离为原点到区域内的点的距离的最小值,即
| 1 | ||
|
∴a2+b2的最小值为
| 1 |
| 5 |
故选C.