数学
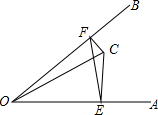
如图，∠AOB=30°，内有一点C，且OC=4，若E，F为边OA、OB上两动点，则△EFC的周长的最小值为多少？

2020-02-25

如图，∠AOB=30°，内有一点C，且OC=4，若E，F为边OA、OB上两动点，则△EFC的周长的最小值为多少？
作业帮
优质解答
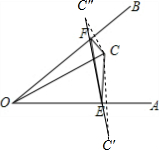作业帮 作点C关于OA对称的点C′，作点C关于OB对称的点C″，连接C′C″，与OA交于点E，与OB交于点F，此时△EFC的周长最小．
从图上可看出△PEF的周长就是C′C″的长，
∵∠AOB=30°，
∴∠C′OC″=60°．
∵OC′=OC″=0C，
∴△OC′C″是等边三角形．
∴C′C″=OC=4．
∴△EFC周长的最小值是4． 作业帮 作点C关于OA对称的点C′，作点C关于OB对称的点C″，连接C′C″，与OA交于点E，与OB交于点F，此时△EFC的周长最小．
从图上可看出△PEF的周长就是C′C″的长，
∵∠AOB=30°，
∴∠C′OC″=60°．
∵OC′=OC″=0C，
∴△OC′C″是等边三角形．
∴C′C″=OC=4．
∴△EFC周长的最小值是4．
相关问答